练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．下列式子：①$\sqrt{{a^2}+{b^2}}$，②$\sqrt{\frac{x}{b}}$，③$\sqrt{{x^2}-xy}$，④$\sqrt{27ab}$中，是最简二次根式的是（　　）
    A．①④B．③④C．①③D．①②

    分析 根据最简二次根式的定义对各选项分析判断后利用排除法求解．

    解答 解：①$\sqrt{{a^2}+{b^2}}$，是最简二次根式；②$\sqrt{\frac{x}{b}}$，不是最简二次根式；③$\sqrt{{x^2}-xy}$，是最简二次根式；④$\sqrt{27ab}$不是最简二次根式，
    故选C

    点评 本题考查最简二次根式的定义．根据最简二次根式的定义，最简二次根式必须满足两个条件：
    （1）被开方数不含分母；
    （2）被开方数不含能开得尽方的因数或因式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

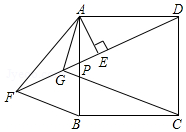    13．如图，正方形ABCD中，P为AB边上任意一点，AE⊥DP于E，点F在DP的延长线上，且EF=DE，连接AF、BF，∠BAF的平分线交DF于G，连接GC．
    （1）求证：△AEG是等腰直角三角形；
    （2）求证：AG+CG=$\sqrt{2}$DG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列运算正确的是（　　）
    A．a3÷a2=a5B．a2•a3=a6C．（ab）3=a3b3D．（a2）3=a5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．若am=4，an=6，则am-n的值为（　　）
    A．$\frac{2}{3}$B．-2C．10D．24

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列运算正确的是（　　）
    A．a3•a3=2a3B．a3+a3=2a6C．a6÷a3=a2D．（-2a2）3=-8a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．若实数a、b、c满足$\sqrt{x+2}$+（y-3）2+|z+6|=0，则xyz的算术平方根是（　　）
    A．36B．±6C．6D．$±\sqrt{6}$

    查看答案和解析>>

    科目：初中数学 来源：2017届广东省揭阳市九年级下学期第一次月考数学试卷（解析版） 题型：单选题

    若点A(3，-8)，B(-2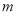， )在同一个反比例函数的图象上，则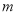值为______.

    查看答案和解析>>

    科目：初中数学 来源：2017届山东省淄博市（五四学制）九年级下学期第一次月考数学试卷（解析版） 题型：判断题

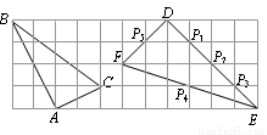
    如图，在边长为1的小正方形组成的网格中，△ABC和△DEF的顶点都在格点上，P1，P2，P3，P4，P5是△DEF边上的5个格点，请按要求完成下列各题：

    （1）试证明三角形△ABC为直角三角形；

    （2）判断△ABC和△DEF是否相似，并说明理由；

    （3）画一个三角形，它的三个顶点为P1，P2，P3，P4，P5中的3个格点并且与△ABC相似；（要求：用尺规作图，保留痕迹，不写作法与证明）

    查看答案和解析>>

    科目：初中数学 来源：2017届山东省济南市天桥区九年级学业水平考试第一次模拟数学试卷（解析版） 题型：解答题

    如图，已知点D在反比例函数y＝的图象上，过点D作x轴的平行线交y轴于点B（0,3）．过点A（5,0）的直线y＝kx＋b与y轴于点C，且BD＝OC，tan∠OAC＝．

    (1)求反比例函数y＝和直线y＝kx＋b的解析式；

    (2)连接CD，试判断线段AC与线段CD的关系，并说明理由；

    (3)点E为x轴上点A右侧的一点，且AE＝OC，连接BE交直线CA与点M，求∠BMC的度数．

    查看答案和解析>>

    同步练习册答案