
【题目】如图,已知抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴上方抛物线上一点,点
轴上方抛物线上一点,点![]() 是直线
是直线![]() 上一点,若
上一点,若![]() 以为顶点的四边形是以
以为顶点的四边形是以 ![]() 为边的平行四边形,求点
为边的平行四边形,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)(0,6)或(-2,4)或(
;(2)(0,6)或(-2,4)或(![]() ,
,![]() ).
).
【解析】
(1)根据待定系数法,即可得到答案;
(2)先求出直线AB的解析式,由平行四边形的性质得AO=MN=3且AO∥MN,设M(x,![]() ),则N(x+3,x+6)或N(x-3,x),根据M,N的纵坐标相等,列出关于x的方程,即可求解.
),则N(x+3,x+6)或N(x-3,x),根据M,N的纵坐标相等,列出关于x的方程,即可求解.
(1)∵抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)设直线AB的解析式为:y=kx+m,
把![]() ,
,![]() ,代入得:
,代入得:![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为:y=x+3.
∵以![]() 为顶点的四边形是以OA为边的平行四边形,
为顶点的四边形是以OA为边的平行四边形,
∴AO=MN=3且AO∥MN,
∵点![]() 是
是![]() 轴上方抛物线上一点,点
轴上方抛物线上一点,点![]() 是直线
是直线![]() 上一点,
上一点,
∴设M(x,![]() ),则N(x+3,x+6)或N(x-3,x),
),则N(x+3,x+6)或N(x-3,x),
∴![]() =x+6或
=x+6或![]() =x,解得:
=x,解得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
令y=0代入![]() ,得:
,得:![]() ,解得:x=-3或x=2,
,解得:x=-3或x=2,
∴抛物线与x轴的另一个交点坐标为(2,0),
∵点![]() 是
是![]() 轴上方抛物线上一点,
轴上方抛物线上一点,
∴点M的横坐标取值范围为:-3<x<2,
∴点M的坐标为:(0,6)或(-2,4)或(![]() ,
,![]() ).
).


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
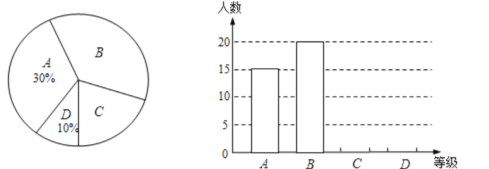
⑴ 九年级(1)班参加体育测试的学生有_________人;
⑵ 将条形统计图补充完整;
⑶ 在扇形统计图中,等级B部分所占的百分比是___,等级C对应的圆心角的度数为___°;
⑷ 若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有___人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的1.5倍,两人各加工300个这种零件,甲比乙少用5天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是150元和120元,现有1500个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费为7800元,那么甲、乙各加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
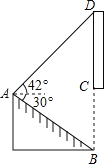
【题目】2021年世界园艺博览会将在扬州枣林湾举办,有一块枣林湾博览会的直传牌CD竖立在路边,其中CB是支柱.小梅同学想计算出CD的长度.于是在A处测得支柱B处的俯角为30°.测得顶端D处的仰角为42°,同时测量出AB的长度是10m,BC的长度是6m.求宜传牌CD的长度(结果保留小数点后一位).(参考数据:![]() ≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
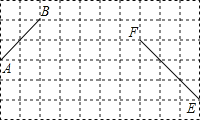
(1)在图中以AB为边画Rt△BAC,点C在小正方形的顶点上,使∠BAC=90°,tan∠ACB=![]() ;
;
(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的顶点上,连接CD、BD,使△BDC是锐角等腰三角形,直接写出∠DBC的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为构建“魅力雨花,和谐雨花,人文雨花”,规划在圭塘河上修建一座观光人行桥(如图1),此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的正规图如图2所示,已知桥面上三组拱桥都为相同的抛物线![]() 的一部分,拱高(抛物线最高点到桥面的距离)为16米,三条抛物线依次与桥面AB相较于点A,C,D,B.
的一部分,拱高(抛物线最高点到桥面的距离)为16米,三条抛物线依次与桥面AB相较于点A,C,D,B.

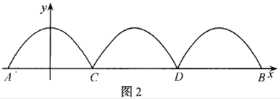
(1)求桥长AB;
(2)已知一组桥拱的造价为a万元,桥面每米的平均造价为b万元.若一组桥拱的造价为整个桥面造价的![]() ,这座观光桥的总造价为504万元,求a,b的值.
,这座观光桥的总造价为504万元,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com