
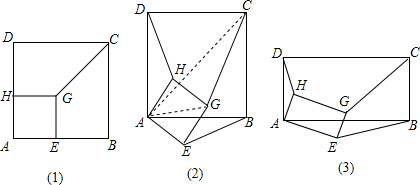
| 2 |
| AE |
| sin45° |
| 2 |
| AB |
| sin45° |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
|
| 2 |
| m2+n2 |
| m2+n2 |
| m2+n2 |


科目:初中数学 来源: 题型:
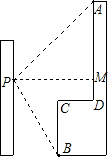 (2012•资阳)小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示).
(2012•资阳)小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•资阳)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接EP、CP、OP.
(2012•资阳)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接EP、CP、OP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com