
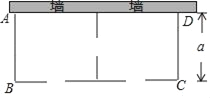
【题目】某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
(1)饲养场的长为多少米(用含a的代数式表示).
(2)若饲养场的面积为288m2,求a的值.
(3)当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?
【答案】(1)60﹣3a;(2)a=12;(3)当a=11时,y最大=297.
【解析】
(1)用总长减去3a后加上三个1米宽的门即为所求;
(2)由(1)表示饲养场面积计算即可,注意a的范围讨论;
(3)设出饲养场面积y与x之间的函数关系,根据已知条件确定自变量a的范围,求函数最大值.
(1)由已知饲养场的长为57﹣2a﹣(a﹣1)+2=60﹣3a;
故答案为:60﹣3a;
(2)由(1)饲养场面积为a(60﹣3a)=288,
解得a=12或a=8;
当a=8时,60﹣3a=60﹣24=36>27,
故a=8舍去,
则a=12;
(3)设饲养场面积为y,
则y=a(60﹣3a)=﹣3a2+60a=﹣3(a﹣10)2+300,
∵2<60﹣3a≤27,
∴11≤a<![]() ,
,
∴当a=11时,y最大=297.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
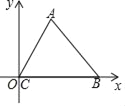
【题目】如图,在直角坐标系中,边长为1的正△ABC(C与O重合)的边BC在x轴上,顶点A在第一象限,现在进行以下操作:
(1)将△ABC沿x轴向右平移一个单位长度,此时A变为A1;
(2)将三角形沿x轴翻折,此时A1变为A2;
(3)将三角形绕点O旋转180°,此时A2变为A3;
(4)将三角形沿y轴翻折,此时A3变为A4;
(5)将三角形绕点O旋转180°,此时A4变为A5;
按照此规律,重复以上五步,则A2018的坐标为( )
A. (![]() ,﹣
,﹣![]() ) B. (﹣
) B. (﹣![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (﹣
) D. (﹣![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
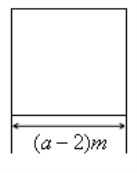
【题目】如图,“丰收1号”小麦的试验田是边长为![]() 米
米![]() 的正方形去掉一个边长为2米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为
的正方形去掉一个边长为2米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为![]() 米的正方形,两块试验田的小麦都收获了
米的正方形,两块试验田的小麦都收获了![]() .
.
(1)哪种小麦的单位面积产量高?
(2)高的单位面积产量是低的单位面积产量的多少倍?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,C,为半径是6的⊙O上两点,点B为![]() 的中点,以线段BA,BC为邻边作菱形ABCD,使点D落在⊙O内(不含圆周上),则下列结论:①直线BD必过圆心O;②菱形ABCD的边长a的取值范围是0<a<10;③若点D与圆心O重合,则∠ABC=120°;④若DO=2,则菱形ABCD的边长为
的中点,以线段BA,BC为邻边作菱形ABCD,使点D落在⊙O内(不含圆周上),则下列结论:①直线BD必过圆心O;②菱形ABCD的边长a的取值范围是0<a<10;③若点D与圆心O重合,则∠ABC=120°;④若DO=2,则菱形ABCD的边长为![]() 或
或![]() .其中正确的是( )
.其中正确的是( )
A. ①③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
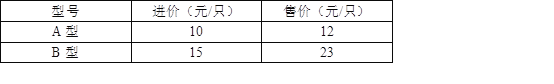
(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
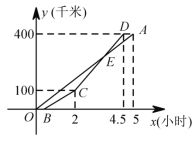
(1)求线段CD对应的函数关系式;
(2)在轿车追上货车后到到达乙地前,何时轿车在货车前30千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
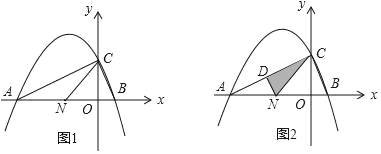
【题目】如图1,抛物线y=﹣![]() x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣
x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣![]() ,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
(1)求出抛物线的解析式,并写出C点的坐标;
(2)试求出当n为何值时,△ANC恰能构成是等腰三角形.
(3)如图2,过N作NF∥BC,与AC相交于D点,连结CN,请问在N点的运动过程中,△CDN的面积是否存在最大值;若存在,试求出该最大面积,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com