Question

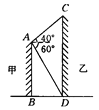
【题目】如图所示，两建筑物的水平距离为24 m，从A点测得D点的俯角为60°，测得C点的仰角为40°，求这两座建筑物的高．(≈1.732，tan 40°≈0.8391，精确到0.01 m)

Answer 1

【答案】61.7l m

【解析】试题分析：过点A作AE⊥CD于点E，可得四边形ABDE为矩形，AB=ED，BD=AE，然后在Rt△AED和Rt△AEC中，分别求出DE和EC的长度，继而可求得建筑物CD的高度和建筑物AB的高度．

试题解析：作AE⊥CD于E，

则AE=BD=24m，

在Rt△AED中，tan∠DAE=，

∴DE=AEtan 60°≈24×1.732≈41.57(m)，

∴AB=DE≈41.57（m）．

在Rt△AEC中，tan∠CAE=,

∴CE=AEtan 40°≈24×0.8391≈20.14(m)，

∴CD=CE＋DE≈20.14＋41.57=61.71(m)，

∴甲建筑物的高AB约为41.57 m，乙建筑物的高CD约为61.7l m．