
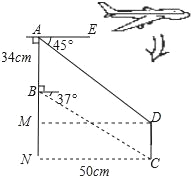
【题目】某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

【答案】22cm.
【解析】试题分析:
如下图,过点D作DM⊥AN于点M,由题意可得∠BCN=37°,CN=50cm,这样在Rt△BCN中,利用∠BCN的正切函数即可计算出BN的长,由AN=AB+BN即可得到AN的长;再证△ADM是等腰直角三角形即可得到AM=MD=NC=50cm,即可由AB=AN-BN计算出AB的长.
试题解析:
作DM⊥AB于M,如图所示,则由题意可知:∠BCN=37°,四边形MDCN是矩形,
∴tan∠BCN=![]() ,MD=CN=50cm,
,MD=CN=50cm,
∴BN=CNtan37°=50×0.75≈37.5(cm),
∴AN=AB+BN=34+37.5=71.5cm,
∵∠DAE=45°,∠BAE=90°,
∴∠DAM=45°,
∴△ADM是等腰直角三角形,
∴AM=DM=50cm,
∴CD=MN=AN﹣AM=71.5﹣50≈22(cm).
答:根据图中的数据求CD的长约为22cm.


科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设①踢毽子;②篮球;③跳绳;④乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下不完整的两个统计图,依据图中信息,得出下列结论中正确的是( )
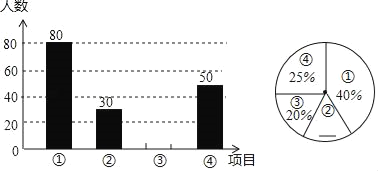
A. 本次共调查300名学生
B. 扇形统计图中,喜欢篮球项目的学生部分所对应的扇形圆心角大小为45°
C. 喜欢跳绳项日的学生人数为60人
D. 喜欢篮球项目的学生人数为30人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B坐标为(-2,1).
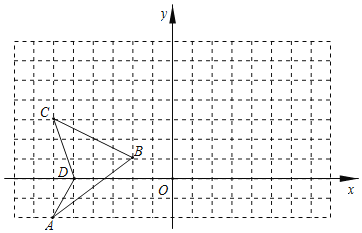
(1)请在图中画出将四边形ABCD关于y轴对称后的四边形A′B′C′D′,并直接写出点A′、B′、C′、D′的坐标;
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
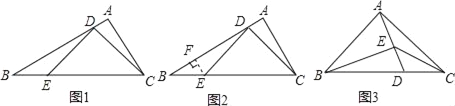
如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明,若不存在,说明理由.
小明通过探究发现,过点E作AB的垂线EF,垂足为F,能得到一对全等三角形(如图2),从而将解决问题.
请回答:
(1)小明发现的与CD相等的线段是_____.
(2)证明小明发现的结论;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,AB=AC,∠BAC=90°,点D在BC上,BD=2DC,点E在AD上,且∠BEC=135°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B 布袋中有三个完全相同的小球,分别标有数字﹣1,﹣2和﹣3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=﹣x﹣1上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙人文教用品商店欲购进![]() 、
、![]() 两种笔记本,用160元购进的
两种笔记本,用160元购进的![]() 种笔记本与用240元购进的
种笔记本与用240元购进的![]() 种笔记本数量相同,每本
种笔记本数量相同,每本![]() 种笔记本的进价比每本
种笔记本的进价比每本![]() 种笔记本的进价贵10元.
种笔记本的进价贵10元.
(1)求![]() 、
、![]() 两种笔记本每本的进价分别为多少元?
两种笔记本每本的进价分别为多少元?
(2)若该商店准备购进![]() 、
、![]() 两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进
两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进![]() 种笔记本多少本?
种笔记本多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2+bx+c过点A(﹣1,0),且经过直线y=x﹣3与坐标轴的两个交点B、C.
(1)求抛物线的表达式;
(2)若点M在第四象限内且在抛物线上,有OM⊥BC,垂足为D,求点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com