
【题目】(1)一个不透明的盒子中装有 2 枚黑色的棋子和 1 枚白色的棋子,每枚棋子除了颜色外其余均相同.从盒中随机摸出一枚棋子,记下颜色后放回并搅匀,再从盒子中随机摸出一枚棋子,记下颜色,用画树状图(或列表)的方法,求两次摸出的棋子颜色不同的概率.
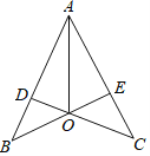
(2)如图,已知 ![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点O,连接
于点O,连接![]() ,求证:AO平分
,求证:AO平分![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的棋子颜色不同的情况,再利用概率公式即可求得答案;
(2)根据已知条件得到△BOD≌△COE,然后得到OD=OE,∠ODB=∠OEC,进而证明△ADO≌△AEO,即可得出答案.
解:(1)画树状图可得:

∵共有9种等可能的结果,两次摸出的棋子颜色不同的有4种情况,
∴两次摸出的棋子颜色不同的概率为:![]() .
.
证明:(2)在△BOD和△COE中

∴△BOD≌△COE(AAS)
∴OD=OE,∠ODB=∠OEC
∠ODA=180°-∠ODB
∠OEA=180°-∠OEC
∴∠ODA=∠OEA
又∵AB=AC,BD=CE
AD=AB-BD
AE=AC-CE
∴AD=AE
在△ADO和△AEO中

∴△ADO≌△AEO(SAS)
∴∠OAD=∠OAE
∴AO平分∠BAC


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
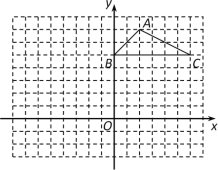
(1) 点A的坐标为 ,点C的坐标为 ;
(2) 将△ABC先向左平移3个单位长度,再向下平移6个单位长度,请画出平移后的△A1B1C1;
(3) 连接A1B,A1 C,△A1BC的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AM∥BN,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA,NB分别相交于点D,E.
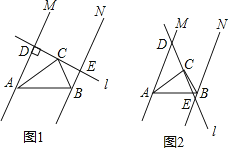
(1)如图1,当直线l与直线MA垂直时,试探究AB,AD,BE之间的数量关系并说明理由;
(2)如图2,当直线l与直线MA不垂直,且交点D,E在AB的异侧时,则(1)的结论还成立吗?若成立,请说明理由;若不成立,请直接写出AB,AD,BE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了建设社会主义新农村,我市积极推进“行政村通畅工程”.A村和B村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间的道路改造.下面能反映该工程尚未改造的道路里程y(公里)与时间x(天)的关系的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)地表以下的岩层的温度和它所处的深度有以下关系:

①上表反映了两个变量之间的关系,哪个是自变量?哪个是因变量?
②深度每增加![]() ,温度增加多少摄氏度?
,温度增加多少摄氏度?
③估计![]() 深处的岩层温度是多少摄氏度.
深处的岩层温度是多少摄氏度.
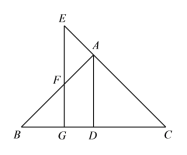
(2)已知:如图,![]() 于
于![]() ,
,![]() 于G,
于G,![]() .
.
求证:![]() 平分
平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连结BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连结BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0) 交x轴正半轴于点A,直线y=2x 经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.
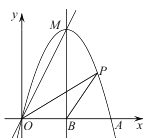
(1)求a,b的值;
(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m ,△OBP的面积为S,![]() .求K关于m 的函数表达式及K的范围.
.求K关于m 的函数表达式及K的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:
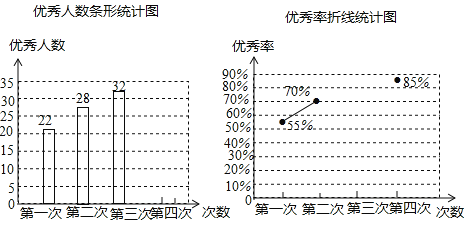
(1)求该班总人数;
(2)根据计算,请你补全两个统计图;
(3)已知该班甲同学四次训练成绩为85,95,85,95,乙同学四次成绩分别为85,90,95,90,现需从甲、乙两同学中选派一名同学参加校级比赛,你认为应该选派哪位同学并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com