
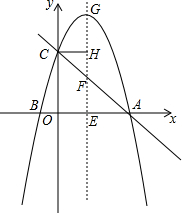
 已知抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于点C,点B的坐标为(-1,0),过x轴上一点E作EG⊥x轴交抛物线于点G,交直线AC于点F.
已知抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于点C,点B的坐标为(-1,0),过x轴上一点E作EG⊥x轴交抛物线于点G,交直线AC于点F.分析 (1)直接利用坐标轴上点的坐标特点即可确定;
(2)先确定出点E坐标,即可得出CH,AE,最后用相似三角形得出的比例式列出方程求解即可;
(3)先判断出∠AFE≠90°,再分两种情况利用等腰直角三角形的性质列出方程或方程组求解即可.
解答 解:(1)令x=0,
∴y=4,
∴C(0,4),
故答案为:0,4;
(2)∵抛物线y=ax2+bx+4与x轴交于A,B(-1,0)两点,
∴a-b+4=0,
∴b=a+4,
∴抛物线的解析式为y=ax2+(a+4)x+4=(ax+4)(x+1)
∴A(-$\frac{4}{a}$,0),对称轴为x=-$\frac{b}{2a}$=-$\frac{a+4}{2a}$,
∵直线EG为抛物线的对称轴,
∴E(-$\frac{a+4}{2a}$,0),
∴OE=|-$\frac{a+4}{2a}$|,
∵EG⊥x,CH⊥GE,
∴CH∥AE,四边形OCHE是矩形,
∴CH=OE=|-$\frac{a+4}{2a}$|,AE=BE=|-$\frac{a+4}{2a}$+1|,
∵CH∥AE,
∴△CHF∽△AEF,
∴$\frac{CH}{AE}=\frac{FH}{FE}$,
∵$\frac{FH}{FE}$=$\frac{3}{5}$,
∴$\frac{|-\frac{a+4}{2a}|}{|-\frac{a+4}{2a}+1|}$=$\frac{3}{5}$,
∴a=-1或a=-16,
∴b=a+4=3或-12,
∴抛物线解析式为y=-x2+3x+4或y=-16x2-12x+4.
(3)∵A(-$\frac{4}{a}$,0),C(0,4),
∴直线AC解析式为y=ax+4,
设E(m,0),
∴F(m,am+4),G(m,am2+(a+4)m+4);
∵△CGF为等腰直角三角形,
∵EG⊥x轴,
∴∠AFE≠90°,
∴①当∠FCG=90°时,
如图,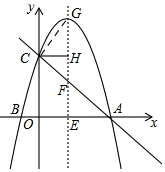 ∴FG=2CH=2OE,点H是FG的中点,且纵坐标和点C的相同,
∴FG=2CH=2OE,点H是FG的中点,且纵坐标和点C的相同,
∴|am2+4m|=|m|①,$\frac{am+4+a{m}^{2}+am+4m+4}{2}$=4②,
联立①②得,a=-$\frac{1}{2}$,m=6或a=$\frac{1}{2}$,m=-6,
∴E(6,0)或(-6,0),
②当∠CGF=90°时,CG=FG,
∵FG⊥x轴,
∴CG∥x轴,
∴G的纵坐标为4,
∴G(-$\frac{a+4}{a}$,4),F(-$\frac{a+4}{a}$,$\frac{4}{a+4}$),E(-$\frac{a+4}{a}$,0),
∴CG=|$\frac{a+4}{4}$|,FG=|4-$\frac{4}{a+4}$|,
∴|$\frac{a+4}{4}$|=|4-$\frac{4}{a+4}$|,
∴a=4+4$\sqrt{3}$或a=4-4$\sqrt{3}$,或a=-12+4$\sqrt{5}$或a=-12-4$\sqrt{5}$,
∴-$\frac{a+4}{a}$=-$\frac{1+\sqrt{3}}{2}$或-$\frac{a+4}{a}$=-$\frac{1-\sqrt{3}}{2}$或-$\frac{a+4}{a}$=$\frac{5\sqrt{5}-11}{4}$ 或-$\frac{a+4}{a}$=-$\frac{1+\sqrt{5}}{4}$,
∴E(-$\frac{1+\sqrt{3}}{2}$,0)或(-$\frac{1-\sqrt{3}}{2}$,0)或( $\frac{5\sqrt{5}-11}{4}$,0)或(-$\frac{1+\sqrt{5}}{4}$,0).
即:满足条件的E的坐标为E(6,0)或(-6,0)或(-$\frac{1+\sqrt{3}}{2}$,0)或(-$\frac{1-\sqrt{3}}{2}$,0)或( $\frac{5\sqrt{5}-11}{4}$,0)或(-$\frac{1+\sqrt{5}}{4}$,0).
点评 此题是二次函数综合题,主要考查了坐标轴上点的特点,相似三角形的性质,等腰直角三角形的性质解方程或方程组,是一道中等难度的试题,但计算量比较大.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
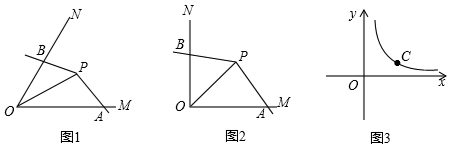 如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.
如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长为6 cm.
八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长为6 cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
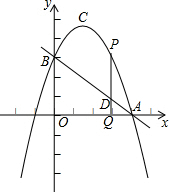 如图,抛物线顶点坐标为点C(2,8),交x轴于点A (6,0),交y轴于点B.
如图,抛物线顶点坐标为点C(2,8),交x轴于点A (6,0),交y轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,△ABC为等边三角形,AB=6cm,D点在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的长.
已知如图,△ABC为等边三角形,AB=6cm,D点在BC上,且∠ADE=60°,$\frac{DB}{DC}$=$\frac{1}{2}$,求AE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com