
定义符号“*”表示的运算法则为a*b=ab+3a,若(3*x)+(x*3)=-27,则x=
A. 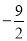 B.
B. 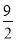 C. 4 D. -4
C. 4 D. -4
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷(解析版) 题型:填空题
已知扇形的圆心角为 ,弧长为
,弧长为 ,则这个扇形的半径为__________
,则这个扇形的半径为__________  .
.
查看答案和解析>>
科目:初中数学 来源:四川省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,已知AB∥CD, 若∠C=35?,AB是∠FAD的平分线.

(1)求∠FAD的度数;
(2)若∠ADB=110?,求∠BDE的度数.
(1)70°;(2)35°. 【解析】试题分析:(1)由AB//CD可得∠C=∠FAB=35°,再根据AB是∠FAD的平分线即可得; (2)由AB//CD可得∠ADC=∠BAD=35°,再根据∠ADB=110°,利用平角的定义即可得. 试题解析:(1)∵AB//CD, ∴∠C=∠FAB=35°, ∵AB是∠FAD的平分线, ∴∠FAB=∠BAD=35°, ...查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2017-2018学年七年级上学期期末数学试卷 题型:解答题
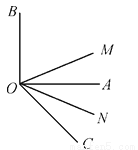
如图,∠AOB是直角,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)当∠AOC=40°,求出∠MON的大小,并写出解答过程理由;
(2)当∠AOC=50°,求出∠MON的大小,并写出解答过程理由;
(3)当锐角∠AOC=α时,求出∠MON的大小,并写出解答过程理由.
查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2017-2018学年七年级上学期期末数学试卷 题型:填空题
如图,数轴上相邻刻度之间的距离是 ,若BC=
,若BC= ,A点在数轴上对应的数值是-
,A点在数轴上对应的数值是- ,则B点在数轴上对应的数值是 ____________.
,则B点在数轴上对应的数值是 ____________.

查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2017-2018学年七年级上学期期末数学试卷 题型:单选题
把方程 的分母化为整数的方程是
的分母化为整数的方程是
A.  B.
B. 
C. 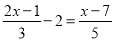 D.
D. 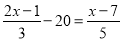
查看答案和解析>>
科目:初中数学 来源:湖南省2018届九年级上学期期末考试数学试卷 题型:解答题
如图,已知抛物线y=- x2+bx+c与x轴交于点A(-1,0)和B,与y轴交于点C(0,3).
(1)求此抛物线的解析式及点B的坐标;
(2)设抛物线的顶点为D,连接CD、DB、CB、AC.
①求证:△AOC∽△DCB;②在坐标轴上是否存在与原点O不重合的点P,使以P、A、C为顶点的三角形与△DCB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由;

查看答案和解析>>
科目:初中数学 来源:湖南省2018届九年级上学期期末考试数学试卷 题型:单选题
两个相似三角形的面积之比为1:9,则相似比为( )
A. 1:9 B. 9:1 C. 1:3 D. 3:1
C 【解析】两个相似三角形的面积之比为1∶9,则相似比为1∶3. 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若
(1)试说明 ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求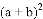 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com