
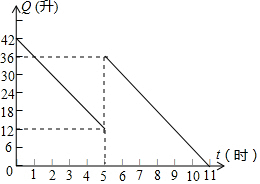
 某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.
某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.分析 (1)观察函数图象,即可得出结论;
(2)根据每小时耗油量=总耗油量÷行驶时间,即可求出机动车每小时的耗油量,再根据加油前油箱剩余油量=42-每小时耗油量×行驶时间,即可得出结论;
(3)根据函数图象中t=5时,Q值的变化,即可求出中途加油量;
(4)根据可行驶时间=油箱剩余油量÷每小时耗油量,即可求出续航时间,由路程=速度×时间,即可求出续航路程,将其与230比较后即可得出结论.
解答 解:(1)观察函数图象可知:机动车行驶5小时后加油.
(2)机动车每小时的耗油量为(42-12)÷5=6(升),
∴加油前油箱剩余油量Q与行驶时间t的函数关系为Q=42-6t(0≤t≤5).
(3)36-12=24(升).
答:中途加油24升.
(4)∵加油后油箱里的油可供行驶11-5=6(小时),
∴剩下的油可行驶6×40=240(千米),
∵240>230,
∴油箱中的油够用.
点评 本题考查了一次函数的应用,解题的关键是:(1)观察函数图象找出结论;(2)根据数量关系,列出函数关系式;(3)根据数量关系,列式计算;(4)利用路程=速度×时间,求出可续航路程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | a=-3 | B. | -4<a<-3 | C. | -4≤a<-3 | D. | -4<a≤-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
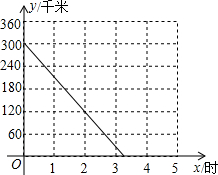 A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条公路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶住B城,乙车驶往A城,甲车在行驶过程中速度始终不变,甲车距B城高速公路入口处的距离y(km)与行驶时间x(h)之间的关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com