
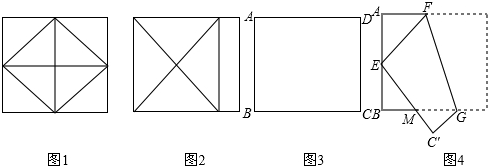
如图8-27,在长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形,通过计算两个图形的面积,验证了一个等式,则这个等式是

图8-27
A.a2-b2=(a-b)(a+b) B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2 D.(a+2b)(a-b)=a2+ab-2b2
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

| 5 |
| FF′ |
| CG′ |
| 2 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
如图,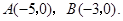 点
点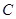 在
在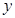 轴的正半轴上,
轴的正半轴上,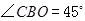 ,
,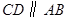 ,
,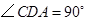 .点
.点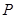 从点
从点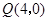 出发,沿
出发,沿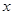 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为 秒.
秒.
求点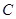 的坐标;
的坐标;
当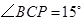 时,求
时,求 的值;
的值;
以点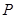 为圆心,
为圆心,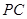 为半径的
为半径的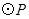 随点
随点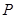 的运动而变化,当
的运动而变化,当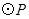 与四边形
与四边形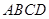
的边(或边所在的直线)相切时,求 的值.
的值.

|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com