

分析 (1)移项、合并同类项即可求解;
(2)去括号、移项、合并同类项、系数化成1即可求解;
(3)把(1)和(2)求得解集在数轴上表示出来即可;
(4)两个解集的公共部分就是不等式组的解集.
解答 解:(1)移项得5x-4x<3,
合并同类项得x<3.
故答案是x<3;
(2)去括号,得4x-4+3≥2x,
移项,得4x-2x≥4-3,
合并同类项得2x≥1,
系数化成1得x≥$\frac{1}{2}$.
故答案是x≥$\frac{1}{2}$;
(3) ;
;
(4)不等式组的解集是:$\frac{1}{2}$≤x<3,
故答案是:$\frac{1}{2}$≤x<3.
点评 本题考查了解一元一次不等式组:求不等式组的解集的过程叫解不等式组.解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:解答题
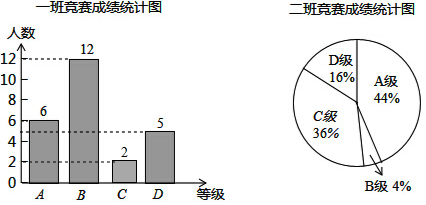
| 平均数(分) | 中位数(分) | 众数(分) | |
| 一班 | 77.6 | 80 | 80 |
| 二班 | 77.6 | 70 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
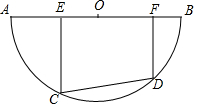 如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.
如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
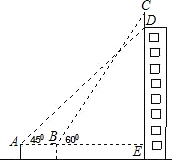 如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)
如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
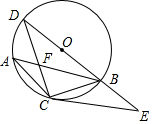 如图,AB是⊙O的弦,C是劣弧$\widehat{AB}$的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.
如图,AB是⊙O的弦,C是劣弧$\widehat{AB}$的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
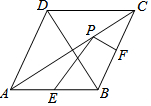 如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )
如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com