
【题目】已知:点![]() 、
、![]() 、
、![]() 不在同一条直线上,
不在同一条直线上,![]() .
.

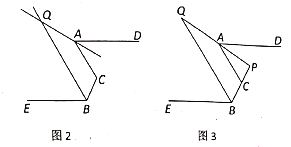
(1)如图1,当![]() ,
,![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图2,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的平分线所在直线,试探究
的平分线所在直线,试探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图3,在(2)的前提下,有![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)∠ACB=120°;(2)2∠AQB+∠C=180°;(3)∠DAC:∠ACB:∠CBE=1:2:2.
【解析】
(1)首先过C作AD的平行线CE,再根据平行的性质计算即可.
(2)首先过点Q作QM∥AD,再根据已知平行线的性质即可,计算的2∠AQB+∠C=180°.
(3)根据平行线的性质和角平分线的性质首先计算出∠DAC、∠ACB、∠CBE,再根据角的度数求比值.
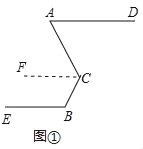
(1)在图①中,过点C作CF∥AD,则CF∥BE.
∵CF∥AD∥BE,
∴∠ACF=∠A,∠BCF=180°﹣∠B,
∴∠ACB=∠ACF+∠BCF=180°﹣(∠B﹣∠A)=120°.
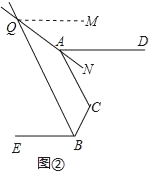
(2)在图2中,过点Q作QM∥AD,则QM∥BE.
∵QM∥AD,QM∥BE,
∴∠AQM=∠NAD,∠BQM=∠EBQ.
∵AQ平分∠CAD,BQ平分∠CBE,
∴∠NAD=![]() ∠CAD,∠EBQ=
∠CAD,∠EBQ=![]() ∠CBE,
∠CBE,
∴∠AQB=∠BQM﹣∠AQM=![]() (∠CBE﹣∠CAD).
(∠CBE﹣∠CAD).
∵∠C=180°﹣(∠CBE﹣∠CAD)=180°﹣2∠AQB,
∴2∠AQB+∠C=180°.
(3)∵AC∥QB,
∴∠AQB=∠CAP=![]() ∠CAD,∠ACP=∠PBQ=
∠CAD,∠ACP=∠PBQ=![]() ∠CBE,
∠CBE,
∴∠ACB=180°﹣∠ACP=180°﹣![]() ∠CBE.
∠CBE.
∵2∠AQB+∠ACB=180°,
∴∠CAD=![]() ∠CBE.
∠CBE.
又∵QP⊥PB,
∴∠CAP+∠ACP=90°,即∠CAD+∠CBE=180°,
∴∠CAD=60°,∠CBE=120°,
∴∠ACB=180°﹣(∠CBE﹣∠CAD)=120°,
∴∠DAC:∠ACB:∠CBE=60°:120°:120°=1:2:2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一个点在第一象限及x轴、y轴上移动,在第一秒钟,它从原点移动到点(1,0),然后按照图中箭头所示方向移动,即(0,0)→(1,0)→(1,1)→)(0,1)→(0,2)→……,且每秒移动一个单位,那么第2018秒时,点所在位置的坐标是( ).

A. (6,44)B. (38,44)C. (44,38)D. (44,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县近两个多月持续高温而且没有降雨导致居民用水严重紧缺,为了加强市民的节水意识,我县制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨2元,超过10吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤10,请写出y与x的函数关系式.
(2)若x>10,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费29元,那么这个月该户用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住集安国际枫叶旅游节的商机,某商店决定购进A、B两种旅游纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元;
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解七年级800名学生期中数学考试情况,从中抽取了100名学生的数学成绩进行了统计.下面5个判断中正确的有( )
①这种调查方式是抽样调查;②800名学生是总体:③每名学生的数学成绩是个体④100名学生是总体的一个样本;⑤样本容量是100
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com