解:(1)设方程9x
2-9xsinA-2=0的两根为x
1,x
2,
则x
1+x
2=sinA,x
1•x
2=-

.
∴x
12+x
22=(x
1+x
2)
2-2x
1•x
2=sin
2A+

.
∵方程9x
2-9xsinA-2=0的两根的平方和是1,
∴sin
2A+

=1,
∴sinA=±

,
∵∠A为锐角,
∴sinA=

.
(2)依题意,知x、y是关于t的一元二次方程t
2-6t+m
2+4m+13=0①的两根,
则△≥0,
∴36-4(m
2+4m+13)≥0,
∴-(m+2)
2≥0,
∴(m+2)
2≤0,
又∵(m+2)
2≥0,
m=-2.
把m=-2代入方程①,得t
2-6t+9=0,
解得t=3,
∴x=y=3,
∴△ABC是等腰三角形.
分两种情况:①∠A是底角;②∠A是顶角.
①当∠A是底角时,如图,△ABC中,AB=BC=3,作底边AB上的高BD,则AB=2AD.

在直角△ABD中,
∵sinA=

,
∴
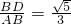
,
∴BD=

,
∴AD=

=2,
∴AC=4;
②当∠A是底角时,如图,△ABC中,AB=AC=3,作腰AC上的高BD.
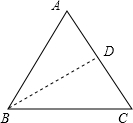
在直角△ABD中,∵sinA=

,
∴
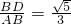
,
∴BD=

,
∴AD=

=2,
∴CD=AC-AD=1.
在直角△ABD中,∵∠BDC=90°,
∴BC=
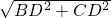
=

.
综上可知,△ABC的第三边的长度为4或

.
分析:(1)根据一元二次方程根与系数的关系及完全平方公式,即可求出sinA的值.
(2)根据根的判别式首先求出m的值,然后分两种情况:①∠A是底角;②∠A是顶角,分别求出△ABC的第三边的长度.
点评:本题主要考查了根的判别式,根与系数的关系,等腰三角形的性质,三角函数的定义,综合性强,难度较大.

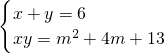 (m为实数),求△ABC的第三边.
(m为实数),求△ABC的第三边. .
. .
. =1,
=1, ,
, .
. 在直角△ABD中,
在直角△ABD中, ,
,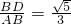 ,
, ,
, =2,
=2, 在直角△ABD中,∵sinA=
在直角△ABD中,∵sinA= ,
,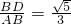 ,
, ,
, =2,
=2,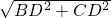 =
= .
. .
.

 阅读快车系列答案
阅读快车系列答案