
【题目】阅读下列两则材料,回答问题,材料一:定义直线y=ax+b与直线y=bx+a互为“共同体直线”,例如,直线y=x+4与直线y=4x+l互为“共同体直线”.
材料二:对于半面直角坐标系中的任意两点P1(x1,y1)、P2(x2,y2),P1、P2之两点间的直角距离d1(P1,p2)=|x1﹣x2|+|y1﹣y2|:例如:Q1(﹣3,1)、Q2(2.4)两点间的直角距离为d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8; P0(x0,y0)为一个定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做Po到直线y=ax+b的直角距离.
(1)计算S(﹣2,6),T(1,3)两点间的直角距离d(S,T)= ,直线y=4x+3上的一点H(a,b)又是它的“共同体直线”上的点,求点H的坐标.
(2)对于直线y=ax+b上的任意一点M(m,n),都有点N(3m,2m﹣3n)在它的“共同体直线”上,试求点L(10,﹣![]() )到直线y=ax+b的直角距离.
)到直线y=ax+b的直角距离.
【答案】(1)d(S,T)=7,H(1,7);(2)10.
【解析】
(1)根据题中所给出的两点的直角距离公式即可得出结论;求两条直线的交点即可求H点的坐标;
(2)先表示直线y=ax+b的“共同体直线”,并将点M和N分别代入可得方程组,得:(3b+3a﹣2)m=﹣a﹣3b,对于任意一点M(m,n)等式均成立,求出a,b的值,再根据题意得出关于x的式子,再由绝对值的几何意义即可得出结论.
解:(1)∵S(﹣2,6)、T(1,3)则S、T两点的直角距离为d(S,T)=|﹣2﹣1|+|6﹣3|=7,
∴S(﹣2,6)、T(1,3)两点间的直角距离d(S,T)=7.
直线y=4x+3的“共同体直线”是y=3x+4,由题意知H是它们的交点,则有:![]() ,
,
解得![]() ,
,
∴点H的坐标为:H(1,7);
(2)∵点M(m,n)是直线y=ax+b上的任意一点,
∴am+b=n①,
∵点N(3m,2m﹣3n)是直线y=ax+b的“共同体直线”上的一点,
即N(3m,2m﹣3n)在直线y=bx+a上
∴3bm+a=2m﹣3n②,
将①代入②得,3bm+a=2m﹣3(am+b),
整理得:3bm+3am﹣2m=﹣a﹣3b,
∴(3b+3a﹣2)m=﹣a﹣3b,
∵对于任意一点M(m,n)等式均成立,
∴![]() ,
,
解得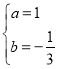 ,
,
![]() .
.
![]() 是直线
是直线![]() 上的动点,定点
上的动点,定点![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() 当
当![]() 时,代数式
时,代数式![]() 有最小值10,
有最小值10,
![]() 点
点![]() 到直线
到直线![]() 的直角距离是10.
的直角距离是10.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】抛物线C:y=![]() x2+bx+c 交
x2+bx+c 交 ![]() 轴于点A(0,-1)且过点
轴于点A(0,-1)且过点 ![]() , P是抛物线C上一个动点,过P作PB∥OA,以P为圆心,2为半径的圆交PB于C、D两点(点D位于点C下方).
, P是抛物线C上一个动点,过P作PB∥OA,以P为圆心,2为半径的圆交PB于C、D两点(点D位于点C下方).
(1)求抛物线C的解析式;
(2)连接AP交⊙P于点E,连接DE,AC.若ΔACP是以CP为直角边的直角三角形,求∠EDC的度数;
(3)若当点P经过抛物线C上所有的点后,点D随之经过的路线被直线 ![]() 截得的线段长为8,求
截得的线段长为8,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“西成高铁”的开通,对于加强关中一天水经济区与成渝经济区的交流合作,促进区域经济发展和提高人民出行质量,具有十分重要的意义.成都某单位组织优秀员工利用周末乘坐“西成高铁”到西安观光旅游,计划游览着名景点“大唐芙蓉园”.已知该景区团体票价格设置如下:
人数/人 | 10人以内(含10人) | 超过10人但不超过30人的部分 | 超过30人的部分 |
单价(元/张) | 120 | 100 | 90 |
(1)求团体票总费用y(元)与游览人数x(人)之间的关系式;
(2)若该单位购买团体票共花费4100元,且所有人都购买了门票,那么该单位共有多少人游览了“大唐芙蓉园”?
查看答案和解析>>
科目:初中数学 来源: 题型:
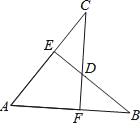
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.
以上结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.

(1)△ODP的面积S=________.
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() 的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.
的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.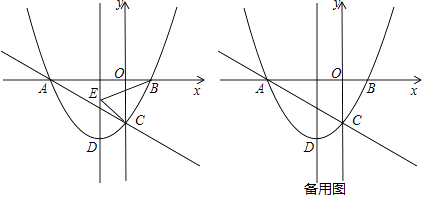
(1)求抛物线顶点 D 的坐标以及直线 AC 的函数表达式;
(2)点 P 是抛物线上一点,且点P在直线 AC 下方,点 E 在抛物线对称轴上,当△BCE 的周长最小时,求△PCE 面积的最大值以及此时点 P 的坐标;
(3)在(2)的条件下,过点 P 且平行于 AC 的直线分别交x轴于点 M,交 y 轴于点N,把抛物线y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() 沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.
沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com