
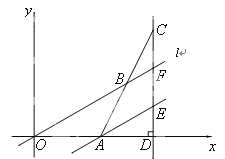
【题目】如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
(1)、若点B的横坐标为6,则点C的坐标为(______,_____),DE的长为 ;
(2)、若点B的横坐标大于3,则线段CF的长度是否发生改变?若不变,请求出线段CF的长度;若改变,请说明理由;
(3)、连结BE,在点B的运动过程中,以OB为直径的⊙P与△ABE某一边所在的直线相切,请求出所有满足条件的DE的长.
【答案】(1)、C(9,![]() );DE=
);DE=![]() ;(2)、证明过程见解析;(3)、DE的长为
;(2)、证明过程见解析;(3)、DE的长为![]() 或
或![]() 或
或![]()
【解析】
试题分析:(1)、根据题意求出点C的坐标及DE的长度;(2)、过点A作AM⊥x轴于M,根据tan∠BOA的值求出AM的长度,然后证明△ABM和△CBF全等,从而得出CG=AM;(3)、本题需要分三种情况进行分类计算,首先分别画出图形,然后分别进行计算.
试题解析:(1)、C(9,![]() ) , DE=
) , DE=![]() ;
;
(2)、如图(1),过点A作AM⊥x轴于M ,∴∠OAM=90°, ∠BOA=30°, ∴AM=OAtan∠BOA=![]() .
.
∵B为AC的中点, ∴AB=BC 又∵AM∥CF, ∴∠AMB=∠CFB ,∠MAB=∠FCB,
∴△ABM≌△CBF ∴CF=AM=![]() . ∴线段CF的长度保持不变.
. ∴线段CF的长度保持不变.
(3)、如图1,过点B作BG⊥x轴于点G.易证, OB=2BG ,CD=2BG,
∴OB=CD.
(I)当点D在点A的右侧时,⊙P只能与BE相切,如图2.
设DE=![]() , 则OB=CD=
, 则OB=CD=![]() . ∵⊙P与BE相切于点B,
. ∵⊙P与BE相切于点B,
∴OB⊥BE. 易得BF=![]() EF=
EF=![]() .
.
∴OF=OB+BF=![]() . ∴OF=2DF, ∴
. ∴OF=2DF, ∴![]() =
=![]() .
.
解得![]() . ∴ DE=
. ∴ DE=![]() .
.
(II)当点D在线段OA上时,①若⊙P与直线AE相切,如图3,
易得,直线l与AE的距离是![]() . ∴ OB=3. ∴ CD=3. ∴DE=2CF-CD=
. ∴ OB=3. ∴ CD=3. ∴DE=2CF-CD=![]() .
.
②当⊙P与AB相切,如图4. ∴∠OBA=90°. ∴OB=OAtan∠OBA=![]() . ∴CD=
. ∴CD=![]() .
.
∴ DE=2CF-CD=![]() =
=![]() .
.
(III)当点D在点O的左侧时,⊙P只能与直线AE相切,如图5 ∵ 直线l与AE的距离是![]() ,
,
∴ OB=3.∴ CD=3. ∴ DE=2CF+CD=![]() .
.
综上所述,DE的长为![]() 或
或![]() 或
或![]() .
.







 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】“五一”期间,某市共接待海内外游客约567000人次,将567000用科学记数法表示为( )
A. 567×103 B. 56.7×104 C. 5.67×105 D. 0.567×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
小明:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
小军:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个十位数字是a,个位数学是b的两位数表示为10a+b,交换这个两位数的十位数字和个位数字,又得一个新的两位数,它是_____,这两个数的差是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

查看答案和解析>>
科目:初中数学 来源: 题型:
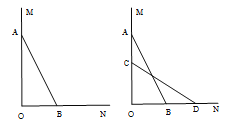
【题目】如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AO上,这时梯足B到墙底端O的距离为0.7米, 如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
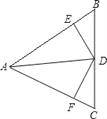
【题目】如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定存款利息的纳税办法是:利息税=利息×5%;银行一年定期储蓄的年利率为2.25%,今年小刚取出一年到期的本金及利息时,交了4.5元的利息税,则小刚一年前存入银行的钱为( )
A.2400元
B.1800元
C.4000元
D.4400元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com