
 如图所示,等腰RT△ABC分别沿着某条直线对称得到图形b,c,d.若上述对称关系保持不变,平移△ABC,使得四个图形能拼成一个既不重叠且无缝隙的正方形,此时点C的坐标为
如图所示,等腰RT△ABC分别沿着某条直线对称得到图形b,c,d.若上述对称关系保持不变,平移△ABC,使得四个图形能拼成一个既不重叠且无缝隙的正方形,此时点C的坐标为| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
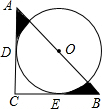 如图,某工件形状如图所示,等腰Rt△ABC中斜边AB=4,点O是AB的中点,以O为圆心的圆分别与两腰相切于点D、E,则图中阴影部分的面积是( )
如图,某工件形状如图所示,等腰Rt△ABC中斜边AB=4,点O是AB的中点,以O为圆心的圆分别与两腰相切于点D、E,则图中阴影部分的面积是( )A、2-
| ||
B、
| ||
C、3-
| ||
| D、2-π |
查看答案和解析>>
科目:初中数学 来源: 题型:044
如图所示,等腰Rt△ABC以2m/s的速度沿直线l向正方形移动,直到AB与CD重合.设x s后,三角形与正方形重叠部分的面积为![]()

(1)写出y与x的关系式;
(2)当x=2,3时,y分别是多少;
(3)当重叠部分的面积是![]() 时,三角形移动了多长时间?
时,三角形移动了多长时间?
查看答案和解析>>
科目:初中数学 来源:2011年广东省深圳市中考数学模拟试卷(05)(解析版) 题型:选择题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com