
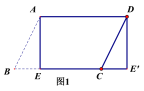
【题目】(1)如图1,纸片![]() ABCD中,AD=5,
ABCD中,AD=5,![]() ,过点A作AE⊥BC,垂足为E,沿AE剪下
,过点A作AE⊥BC,垂足为E,沿AE剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() ,则四边形
,则四边形![]() 的形状为(_____)
的形状为(_____)
A.平行四边形 B.菱形 C.矩形 D.正方形
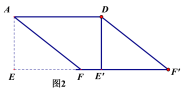
(2)如图2,在(1)中的四边形![]() 中,在EF上取一点P,EP=4,剪下
中,在EF上取一点P,EP=4,剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() 。①求证:四边形
。①求证:四边形![]() 是菱形;②求四边形
是菱形;②求四边形![]() 的两条对角线的长。
的两条对角线的长。
【答案】C
【解析】
(1)根据矩形的判定方法即可判定;
(2)①通过计算证明AF=AD=5,证明四边形AFF′D是平行四边形即可;
②连接AF',DF,分别利用勾股定理计算即可;
(1)解:如图1中,
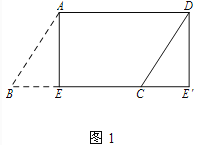
∵四边形ABCD是平行四边形,
∴AD=BC,
∵BE=CE′,
∴AD∥EE′,AD=EE′,
∴四边形AEE′D是平行四边形,
∵∠AEE′=90°,
∴四边形AEE′D是矩形,
故选C.
(2)如图2中,
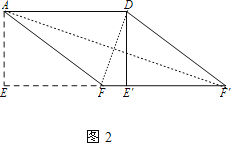
①证明:∵AD=5,S□ABCD=15,
∴AE=3.
又∵在图2中,EF=4,
∴在Rt△AEF中,AF═5.
∴AF=AD=5,
又∵AF∥DF',AF=DF,
∴四边形AFF′D是平行四边形.
∴四边形AFF′D是菱形.
②解:连接AF′,DF,
在Rt△DE′F中,
∵E′F=E′E-EF=5-4=1,DE′=3,
∴DF=![]()
在Rt△AEF′中,
∵E′F=E′E+E′F′=5+4=9,AE=3,
∴AF′=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( ) 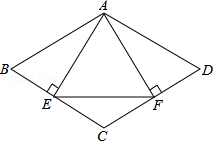
A.4 ![]()
B.3 ![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
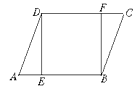
【题目】如图,在平行四边ABCD中,E、F分别是AB、DC上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2) 当∠DEB=90°时,试说明四边形DEBF为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC. 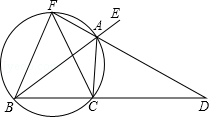
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
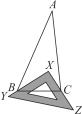
【题目】(1)如图,一个直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C,△ABC中,若∠A=30°,则∠ABC+∠ACB=__ __,∠XBC+∠XCB=__ __;
(2)若改变直角三角板XYZ的位置,但三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否变化?若变化,请说明理由;若不变化,请求出∠ABX+∠ACX的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ACO以O点为中心,逆时针旋转90°,得Rt△BDO,点B坐标为(0,﹣3),点C坐标为(0, ![]() ),抛物线y=﹣
),抛物线y=﹣ ![]() x2+bx+c经过点A和点C.
x2+bx+c经过点A和点C.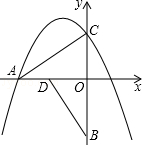
(1)求b,c的值;
(2)在x轴以上的抛物线对称轴上是否存在点Q,使得△ACQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由
(3)点P从点O出发沿x轴向负半轴运动,每秒1个单位,过点P作y轴的平行线交抛物线于点M,当t为几秒时,以M、P、O、C为顶点得四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.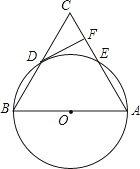
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求 ![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com