
”¾ĢāÄæ”æĖę×Å»„ĮŖĶų”¢ŅʶÆÖÕ¶ĖµÄŃøĖŁ·¢Õ¹£¬Źż×Ö»ÆŌĶĮŌ½Ą“Ō½ĘÕ¼°£¬¹«½»”¢µŲĢśÉĻµÄ”°µĶĶ·×å”±Ō½Ą“Ō½¶ą£¬Ä³ŃŠ¾æ»ś¹¹Õė¶Ō”°ÄśČēŗĪæ““żŹż×Ö»ÆŌĶĮ”±ĪŹĢā½ųŠŠĮĖĖ껜ĪŹ¾ķµ÷²é£ØĪŹ¾ķµ÷²é±ķČēĻĀĶ¼ĖłŹ¾£©£¬²¢½«µ÷²é½į¹ū»ęÖĘ³ÉĶ¼¢ŁŗĶĶ¼¢ŚĖłŹ¾µÄĶ³¼ĘĶ¼£Ø¾ł²»ĶźÕū£©£®
”°ÄśČēŗĪæ““żŹż×Ö»ÆŌĶĮ”±ĪŹ¾ķµ÷²é±ķ
ÄśŗĆ£”ÕāŹĒŅ»·Ż¹ŲÓŚ”°ÄśČēŗĪæ““żŹż×Ö»ÆŌĶĮĪŹ¾ķµ÷²é±ķ£¬ĒėŌŚ±ķøńÖŠŃ”ŌńŅ»ĻīÄś×īČĻĶ¬µÄ¹Ūµć£¬ŌŚĘäŗóæÕøńÄŚ“ņ”°”Ģ”±£¬·Ē³£øŠŠ»ÄśµÄŗĻ×÷£®
“śĀė | ¹Ūµć | |
| »ńČ”ŠÅĻ¢·½±ć£¬æÉŅŌĖꏱĖęµŲ¹Ūæ“ | |
| ¼Ūøń±ćŅĖŅ×µĆ | |
| Ź¹µĆČĖĆĒ³ÉĪŖ”°µĶĶ·×å”±£¬²»ĄūÓŚČĖ¼Ź½»Ķł | |
| ÄŚČŻ·įø»£¬±ČÖ½ÖŹŹéÉęĮŌøü¹ć | |
| ĘäĖū | |
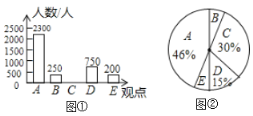
Ēėøł¾ŻĶ³¼ĘĶ¼ÖŠĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£ØI£©±¾“Ī½ÓŹÜµ÷²éµÄ×ÜČĖŹżŹĒ__________ČĖ£¬²¢½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£®
£Ø¢ņ£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬¹Ūµć![]() µÄ°Ł·Ö±ČŹĒ___________£¬±ķŹ¾¹Ūµć
µÄ°Ł·Ö±ČŹĒ___________£¬±ķŹ¾¹Ūµć![]() µÄÉČŠĪµÄŌ²ŠÄ½Ē¶ČŹżĪŖ_________¶Č£®
µÄÉČŠĪµÄŌ²ŠÄ½Ē¶ČŹżĪŖ_________¶Č£®
£Ø¢ó£©Ä³ŹŠ¹²ÓŠ![]() ĶņČĖ£¬Ēėøł¾ŻŅŌÉĻµ÷²é½į¹ū¹ĄĖćøĆŹŠ³Ö
ĶņČĖ£¬Ēėøł¾ŻŅŌÉĻµ÷²é½į¹ū¹ĄĖćøĆŹŠ³Ö![]() £¬
£¬![]() £¬
£¬![]() ¹ŪµćŌŽ³ÉŹż×Ö»ÆŌĶĮµÄČĖŹż¹²ÓŠ¶ąÉŁĶņČĖ£®
¹ŪµćŌŽ³ÉŹż×Ö»ÆŌĶĮµÄČĖŹż¹²ÓŠ¶ąÉŁĶņČĖ£®
”¾“š°ø”æ£ØI£©![]() £»Ķ¼¼ū½āĪö£»£Ø¢ņ£©
£»Ķ¼¼ū½āĪö£»£Ø¢ņ£©![]() £»
£»![]() £»£Ø¢ó£©198Ķņ
£»£Ø¢ó£©198Ķņ
”¾½āĪö”æ
£ØI£©ÓÉA¹ŪµćµÄČĖŹż¼°ĘäĖłÕ¼°Ł·Ö±ČæɵĆ×ÜČĖŹż£¬ŌŁøł¾Żø÷¹ŪµćµÄČĖŹżÖ®ŗĶµČÓŚ×ÜČĖŹżĒó³öCµÄČĖŹż¼“æɲ¹Č«Ķ³¼ĘĶ¼£»
£Ø¢ņ£©ÓĆE¹ŪµćµÄČĖŹż³żŅŌ×ÜČĖŹżæÉĒóµĆEĖłÕ¼°Ł·Ö±Č£¬ÓĆ360”ć³ĖŅŌB¹ŪµćČĖŹżĖłÕ¼±ČĄżæÉĒó³ö¶ŌÓ¦ÉČŠĪµÄŌ²ŠÄ½Ē¶ČŹż£»
£Ø¢ó£©ÓĆ×ÜČĖŹż³ĖŅŌA”¢B”¢D¹ŪµćČĖŹżÕ¼±»µ÷²éČĖŹżµÄ±ČĄż¼“æÉµĆ£®
½ā£ŗ£ØI£©±¾“Ī½ÓŹÜµ÷²éµÄ×ÜČĖŹżŹĒ£ŗ2300”Ā46%£½5000£ØČĖ£©£¬
C¹ŪµćµÄČĖŹżĪŖ50002300250750200£½1500£ØČĖ£©£¬
²¹Ķ¼ČēĻĀ£ŗ

¹Ź“š°øĪŖ£ŗ5000£»
£Ø¢ņ£©¹ŪµćEµÄ°Ł·Ö±ČŹĒ£ŗ![]() ”Į100%£½4%£¬
”Į100%£½4%£¬
±ķŹ¾¹ŪµćBµÄÉČŠĪµÄŌ²ŠÄ½Ē¶ČŹżĪŖ£ŗ360”ć”Į![]() £½18”ć£¬
£½18”ć£¬
¹Ź“š°øĪŖ£ŗ4%£¬18£»
£Ø¢ó£©300”Į![]() £½198£ØĶņČĖ£©£¬
£½198£ØĶņČĖ£©£¬
“š£ŗ¹Ą¼ĘøĆŹŠ³ÖA”¢B”¢D¹ŪµćŌŽ³ÉŹż×Ö»ÆŌĶĮµÄČĖŹż¹²ÓŠ198Ķņ.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¾£³µÖŠŃ§¾ö¶ØŌŚ±¾Š£Ń§ÉśÖŠ£¬æŖÕ¹×ćĒņ”¢ĄŗĒņ”¢ÓšĆ«Ēņ”¢Ę¹ÅŅĒņĖÄÖÖ»ī¶Æ.ĪŖĮĖĮĖ½āѧɜ¶ŌÕāĖÄÖÖ»ī¶ÆµÄĻ²°®Ēéæö£¬Ń§Š£Ė껜µ÷²éĮĖøĆŠ£![]() Ćūѧɜ£¬æ“ĖūĆĒĻ²°®ÄÄŅ»ÖÖ»ī¶Æ£ØĆæĆūѧɜ±ŲŃ”Ņ»ÖÖĒŅÖ»ÄÜ“ÓÕāĖÄÖÖ»ī¶ÆÖŠŃ”ŌńŅ»ÖÖ£©£¬ĻÖ½«µ÷²éµÄ½į¹ū»ęÖĘ³ÉČēĻĀ²»ĶźÕūµÄĶ³¼ĘĶ¼.
Ćūѧɜ£¬æ“ĖūĆĒĻ²°®ÄÄŅ»ÖÖ»ī¶Æ£ØĆæĆūѧɜ±ŲŃ”Ņ»ÖÖĒŅÖ»ÄÜ“ÓÕāĖÄÖÖ»ī¶ÆÖŠŃ”ŌńŅ»ÖÖ£©£¬ĻÖ½«µ÷²éµÄ½į¹ū»ęÖĘ³ÉČēĻĀ²»ĶźÕūµÄĶ³¼ĘĶ¼.

£Ø1£©![]() _____________£¬
_____________£¬![]() _______________£»
_______________£»
£Ø2£©Ēė²¹Č«ÉĻĶ¼ÖŠµÄĢõŠĪĶ¼£»
£Ø3£©øł¾Ż³éŃłµ÷²éµÄ½į¹ū£¬Ēė¹ĄĖćČ«Š£1800Ćūѧɜ֊£¬“óŌ¼ÓŠ¶ąÉŁČĖĻ²°®×ćĒņ£»
£Ø4£©ŌŚ³é²éµÄ![]() Ćūѧɜ֊£¬Ļ²°®“ņĘ¹ÅŅĒņµÄÓŠ10ĆūĶ¬Ń§£ØĘäÖŠÓŠ4ĆūÅ®Éś£¬°üĄØŠ”ŗģ”¢Š”Ć·£©£®ĻÖ½«Ļ²°®“ņĘ¹ÅŅĒņµÄĶ¬Ń§Ę½¾ł·Ö³ÉĮ½×é½ųŠŠŃµĮ·£¬Ö»Å®ÉśĆæ×é·ÖĮ½ČĖ£®ĒóŠ”ŗģ”¢Š”Ć·ÄÜ·ÖŌŚĶ¬Ņ»×éµÄøÅĀŹ£®
Ćūѧɜ֊£¬Ļ²°®“ņĘ¹ÅŅĒņµÄÓŠ10ĆūĶ¬Ń§£ØĘäÖŠÓŠ4ĆūÅ®Éś£¬°üĄØŠ”ŗģ”¢Š”Ć·£©£®ĻÖ½«Ļ²°®“ņĘ¹ÅŅĒņµÄĶ¬Ń§Ę½¾ł·Ö³ÉĮ½×é½ųŠŠŃµĮ·£¬Ö»Å®ÉśĆæ×é·ÖĮ½ČĖ£®ĒóŠ”ŗģ”¢Š”Ć·ÄÜ·ÖŌŚĶ¬Ņ»×éµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
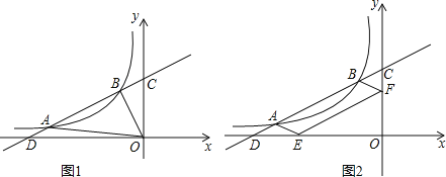
”¾ĢāÄæ”æ ČēĶ¼£¬Ņ»“ĪŗÆŹży=0.5x+3µÄĶ¼ĻóÓė·“±ČĄżŗÆŹży=![]() £Øk”Ł0£©µÄĶ¼Ļó½»ÓŚA£Ø-5£¬a£©£¬BĮ½µć£¬ÓėxÖį½»ÓŚµćD£¬ÓėyÖį½»ÓŚµćC£¬ĒŅAD=BC£®
£Øk”Ł0£©µÄĶ¼Ļó½»ÓŚA£Ø-5£¬a£©£¬BĮ½µć£¬ÓėxÖį½»ÓŚµćD£¬ÓėyÖį½»ÓŚµćC£¬ĒŅAD=BC£®
£Ø1£©Ēó“Ė·“±ČĄżŗÆŹżµÄ±ķ“ļŹ½ŗĶBµć×ų±ź£»
£Ø2£©Į¬½ÓAOŗĶBO£¬ČōµćPŌŚxÖįÉĻ£¬ĒŅS”÷BDP=![]() S”÷BOA£¬ĒóµćPµÄ×ų±ź£»
S”÷BOA£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ČēĶ¼2£¬×÷ABFE£¬µćFŗĶµćE·Ö±šŌŚyÖįŗĶxÖįÉĻ£¬ĒóÖ¤£ŗ”ĻAED=”ĻFEO£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży=3x2+2x+n£¬µ±×Ō±äĮæxµÄȔֵŌŚ-1”Üx”Ü1µÄ·¶Ī§ÄŚŹ±£¬ŗÆŹżÓėxÖįÓŠĒŅÖ»ÓŠŅ»øö¹«¹²µć£¬ŌņnµÄȔֵ·¶Ī§ŹĒ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
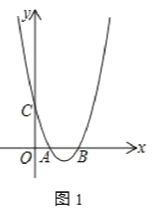
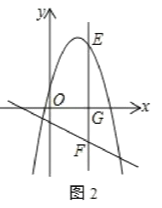
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży=x2+bx+c£¬ĘäĶ¼ĻóÅ×ĪļĻß½»xÖįÓŚµćA(1£¬0)”¢B(3£¬0)£¬½» yÖįÓŚµćC£¬Ö±Ļßl¹żµćC£¬ĒŅ½»Å×ĪļĻßÓŚĮķŅ»µćE(µćE²»ÓėµćA”¢BÖŲŗĻ)£®
(1)Ö±½ÓŠ“³ö¶ž“ĪŗÆŹżµÄ½āĪöŹ½£»
(2)ČōÖ±Ļßl1¾¹żÅ×ĪļĻ߶„µćD£¬½»xÖįÓŚµćF£¬ĒŅl1”Īl£¬ŌņŅŌµćC”¢D”¢E”¢FĪŖ¶„µćµÄĖıߊĪÄÜ·ńĪŖĘ½ŠŠĖıߊĪ£¬ČōÄÜ£¬Ēó³öµćEµÄ×ų±ź£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£»
(3)½«“ĖÅ×ĪļĻßŃŲ×Åy=2·ÕŪ£¬EĪŖĖłµĆŠĀÅ×ĪļĻßxÖįÉĻ·½Ņ»¶Æµć£¬¹żE×÷xÖįµÄ“¹Ļߣ¬½»xÖįÓŚG£¬½»Ö±Ļßy=-![]() x-1ÓŚµćF£¬Ēó
x-1ÓŚµćF£¬Ēó![]() µÄ×ī“óÖµ£®
µÄ×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCŹĒµČ±ßČż½ĒŠĪ£¬µćD”¢E·Ö±šŌŚBC”¢ACÉĻ£¬ĒŅBD=CE£¬ADÓėBEĻą½»ÓŚµćF£®
£Ø1£©ŹŌĖµĆ÷”÷ABD”Õ”÷BCE£»
£Ø2£©”÷EAFÓė”÷EBAĻąĖĘĀš£æĖµĖµÄćµÄĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
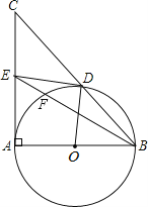
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻBAC=90”ć£¬ABŹĒ”ŃOµÄÖ±¾¶£¬”ŃO½»BCÓŚµćD£¬EĪŖACµÄÖŠµć£¬BE½»”ŃOÓŚµćF£®
£Ø1£©ĒóÖ¤£ŗDEŹĒ”ŃOµÄĒŠĻߣ®
£Ø2£©¢Łµ±”ĻB=______Ź±£¬ĖıߊĪAODEŹĒÕż·½ŠĪ£»
¢ŚŌŚ¢ŁµÄĢõ¼žĻĀ£¬ČōOA=2£¬Ļ߶ĪBFµÄ³¤ĪŖ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚABCDÖŠ£¬![]() £¬
£¬![]() µÄĘ½·ÖĻßÓėDC½»ÓŚµćE£¬
µÄĘ½·ÖĻßÓėDC½»ÓŚµćE£¬![]() £¬BFÓėADµÄŃÓ³¤Ļß½»ÓŚµćF£¬ŌņBCµČÓŚ
£¬BFÓėADµÄŃÓ³¤Ļß½»ÓŚµćF£¬ŌņBCµČÓŚ![]() ””””
””””![]()

A. 2 B. ![]() C. 3 D.
C. 3 D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ŗÆŹży£½![]() £Øx£¾0£©µÄĶ¼ĻóÓėÖ±Ļßy£½x©2½»ÓŚµćA£Ø3£¬m£©£®
£Øx£¾0£©µÄĶ¼ĻóÓėÖ±Ļßy£½x©2½»ÓŚµćA£Ø3£¬m£©£®
£Ø1£©Ēók£¬mµÄÖµ£»
£Ø2£©ŅŃÖŖµćP£Øn£¬n£©£Øn£¾0£©£¬¹żµćP×÷Ę½ŠŠÓŚxÖįµÄÖ±Ļߣ¬½»Ö±Ļßy£½x©2ÓŚµćM£¬¹żµćP×÷Ę½ŠŠÓŚxÖįµÄÖ±Ļß½»ŗÆŹży£½![]() £Øx£¾0£©xµÄĶ¼ĻóÓŚµćN£®
£Øx£¾0£©xµÄĶ¼ĻóÓŚµćN£®
¢Łµ±n£½3Ź±£¬ÅŠ¶ĻĻ߶ĪPMÓėPNµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
¢ŚČōPN”ŻPM£¬½įŗĻŗÆŹżµÄĶ¼Ļó£¬Ö±½ÓŠ“³önµÄȔֵ·¶Ī§£®
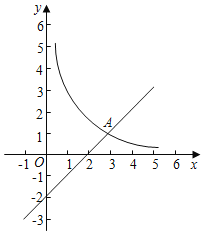
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com