
 在Rt△ABC中,AB=BC,∠ABC=90°,以AB为直径作半圆O,P是BC边上一动点(不与B、c重合),过点P作半圆O的切线,与过A点的垂线交于点Q.AC与PQ,OQ分别交于点E,F,如果P,C,F三点构成的三角形与△AEO相似,那么∠CPF的度数是90°或60°.
在Rt△ABC中,AB=BC,∠ABC=90°,以AB为直径作半圆O,P是BC边上一动点(不与B、c重合),过点P作半圆O的切线,与过A点的垂线交于点Q.AC与PQ,OQ分别交于点E,F,如果P,C,F三点构成的三角形与△AEO相似,那么∠CPF的度数是90°或60°. 分析 解根据等腰直角三角形的性质得到∠C=∠BAC=45°,①当∠CPF=∠AEO时,如图1,得到∠AQG=∠AEO,根据切线的性质得到∠AQE=$\frac{1}{2}∠$AQE,等量代换得到∠AQE=$\frac{1}{2}$∠AEO,求得∠QAE=$\frac{1}{2}∠$AEO,得到结论;②当∠CPF=∠AOE时,如图2,根据平行线的性质得到∠AQP+∠BPQ=180°,根据切线的性质得到∠OQP+∠OPQ=$\frac{1}{2}$(∠AQP+∠BPQ)=90°,等量代换得到∠OPQ=∠AOQ=∠OBP,于是得到结论.
解答 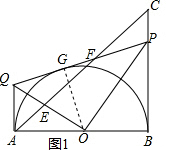 解:∵∠ABC=90°,AQ⊥AB,AB为半圆O的直径,
解:∵∠ABC=90°,AQ⊥AB,AB为半圆O的直径,
∴AQ与BC是半圆O的切线,
∴AQ∥BC,
∵在Rt△ABC中,AB=BC,∠ABC=90°,
∴∠C=∠BAC=45°,
∵P,C,F三点构成的三角形与△AEO相似,
∴①当∠CPF=∠AEO时,如图1,
∴∠AQG=∠AEO,
∵AQ,GQ是半圆O的切线,
∴∠AQE=$\frac{1}{2}∠$AQE,
∴∠AQE=$\frac{1}{2}$∠AEO,
∵∠AEO=∠AQE+∠QAE,
∴∠QAE=$\frac{1}{2}∠$AEO,
∵∠QAE=45°,
∴∠AEO=90°,
∴∠CPF=90°;
②当∠CPF=∠AOE时,如图2,
∵AQ∥BC,
∴∠AQP+∠BPQ=180°,
∵PQ,AQ,BP是半圆O的切线,
∴∠OQP+∠OPQ=$\frac{1}{2}$(∠AQP+∠BPQ)=90°,
∴∠OPQ=∠AOQ=∠OBP,
∴∠CPF=∠FPO=∠BPO=60°.
综上所述:如果P,C,F三点构成的三角形与△AEO相似,那么∠CPF的度数是90°或60°,
故答案为:90°或60°.
点评 本题考查了相似三角形的判定,等腰直角三角形的性质,切线的性质,熟练掌握切线的性质是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,E为AB的中点.DF⊥CE.若AD=8.AB=4.则CF=$\frac{4\sqrt{17}}{17}$,DF=$\frac{16\sqrt{17}}{17}$.
如图,矩形ABCD中,E为AB的中点.DF⊥CE.若AD=8.AB=4.则CF=$\frac{4\sqrt{17}}{17}$,DF=$\frac{16\sqrt{17}}{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
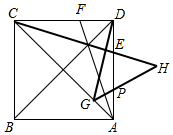 在正方形ABCD中,DE=DF,DG⊥CE,交CA于G,GH⊥AF,交AD于P,交CE延长线于H,请问三条粗线DG,GH,CH的数量关系.
在正方形ABCD中,DE=DF,DG⊥CE,交CA于G,GH⊥AF,交AD于P,交CE延长线于H,请问三条粗线DG,GH,CH的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com