
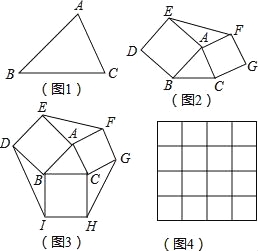
【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.
(1)用尺规将图1中的△ABC分割成两个互补三角形;
(2)证明图2中的△ABC分割成两个互补三角形;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI.
①已知三个正方形面积分别是17、13、10,在如图4的网格中(网格中每个小正方形的边长为1)画出边长为![]() 、
、![]() 、
、![]() 的三角形,并计算图3中六边形DEFGHI的面积.
的三角形,并计算图3中六边形DEFGHI的面积.
②若△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积.
【答案】(1)作图见解析(2)证明见解析(3)①62;②6
【解析】
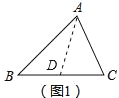
试题分析:(1)作BC边上的中线AD即可.
(2)根据互补三角形的定义证明即可.
(3)①画出图形后,利用割补法求面积即可.
②平移△CHG到AMF,连接EM,IM,则AM=CH=BI,只要证明S△EFM=3S△ABC即可.
试题解析:(1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形.
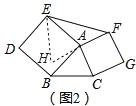
(2)如图2中,延长FA到点H,使得AH=AF,连接EH.
∵四边形ABDE,四边形ACGF是正方形,
∴AB=AE,AF=AC,∠BAE=∠CAF=90°,
∴∠EAF+∠BAC=180°,
∴△AEF和△ABC是两个互补三角形.
∵∠EAH+∠HAB=∠BAC+∠HAB=90°,
∴∠EAH=∠BAC,
∵AF=AC,
∴AH=AB,
在△AEH和△ABC中,
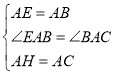
∴△AEH≌△ABC,
∴S△AEF=S△AEH=S△ABC.
(3)①边长为![]() 、
、![]() 、
、![]() 的三角形如图4所示.
的三角形如图4所示.
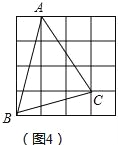
∵S△ABC=3×4﹣2﹣1.5﹣3=5.5,
∴S六边形=17+13+10+4×5.5=62.
②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,
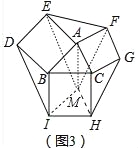
∵AM∥CH,CH⊥BC,
∴AM⊥BC,
∴∠EAM=90°+90°﹣x=180°﹣x,
∵∠DBI=360°﹣90°﹣90°﹣x=180°﹣x,
∴∠EAM=∠DBI,∵AE=BD,
∴△AEM≌△DBI,
∵在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,
∴△DBI和△ABC是互补三角形,
∴S△AEM=S△AEF=S△AFM=2,
∴S△EFM=3S△ABC=6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如图:
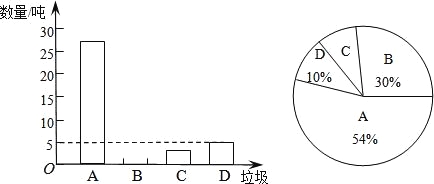
(注:A为可回收物,B为厨余垃圾,C为有害垃圾,D为其他垃圾)
根据图表解答下列问题:
(1)在抽样数据中,产生的有害垃圾共多少吨?
(2)请将条形统计图补充完整;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.多边形的内角和为360°
B.若2a﹣b=1,则代数式6a﹣3b﹣3=0
C.二次函数y=(x﹣1)2+2的图象与y轴的交点的坐标为(0,2)
D.矩形的对角线互相垂直平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达。已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个锐角的余角比这个角的补角小90°;
B. 如果一个角有补角,那么这个角必是钝角;
C. 若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角;
D. 如果∠α和∠β互为余角,∠β与∠θ互为余角,那么∠α与∠θ互为余角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列判断:①在数轴上,原点两旁的两个点所表示的数都是互为相反数;②任何正数必定大于它的倒数;③5ab, ![]() ,
, ![]() 都是整式;④x2﹣xy+y2是按字母y的升幂排列的多项式,其中判断正确的是( )
都是整式;④x2﹣xy+y2是按字母y的升幂排列的多项式,其中判断正确的是( )
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,将直线l向右平移1个单位长度得到的直线解析式是y=2x+2,则原来的直线解析式是( )
A. y=3x+2 B. y=2x+4 C. y=2x+1 D. y=2x+3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com