
【题目】如图,是将抛物线y=-x2 平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0) ,另一交点为B,与y轴交点为C.
(1)求抛物线的函数表达式;
(2)若点N 为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=![]() x+
x+![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.

【答案】(1)y=-x2+2x+3;(2)(1,4); (3)P、Q的坐标是(0,3)(1,3) 或![]() ,
,![]() .
.
【解析】试题分析:
(1)由题意可设该抛物线的解析式为![]() ,代入点(-1,0)求出k的值即可得到所求解析式;
,代入点(-1,0)求出k的值即可得到所求解析式;
(2)由(1)中所得抛物线的解析式可求得点B、C的坐标,从而可求出直线BC的解析式,由直线NC⊥BC且过点C可求得NC的解析式,把NC的解析式和抛物线的解析式联立得到方程组,解方程组即可求得点N的坐标;
(3)如下图,由题意易得PQ=OA=1,且PQ∥OA,设点P的横坐标为t,则可用含“t”的式子表达出Q的坐标,再把Q的坐标代入函数y=![]() x+
x+![]() 中,即可解得“t”的值,从而可求得P、Q的坐标.
中,即可解得“t”的值,从而可求得P、Q的坐标.
试题解析:
(1)设抛物线的解析式是y=-(x-1)2+4.把 (-1,0)代入得 0=-(1-1)2+k,
解得,k=4
则抛物线的解析式是 y=-(x-1)2+4,
即y=-x2+2x+3;
(2)设直线BC的解析式为y=kx+b(k≠0),代入点B、C的坐标得:
![]() 解得:
解得: ![]() ,
,
∴直线BC的解析式为:y=-x+3,
∵BC⊥NC,
∴可设直线CN的解析式为y=x+m.
∵C(0,3)在直线CN上,
∴0+m=3,解得:m=3,即直线CN的解析式为 y=x+3,
由: ![]() ,即 x+3=-x2+2x+3=-x2+2x+3,解得:x1=0,x2=1,
,即 x+3=-x2+2x+3=-x2+2x+3,解得:x1=0,x2=1,
∴N的坐标是(1,4),

(3)∵四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,
设P(t,-t2+2t+3),则Q(t+1, -t2+2t+3) ,将P、Q的坐标代入![]() ,
,
得-t2+2t+3=![]() ,
,
整理,得2t2-t=0, ,
解得t=0 或![]() .
.
∴-t2+2t+3 的值为3或![]() .
.
∴P、Q的坐标是(0,3)(1,3) 或![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
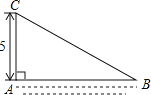
【题目】如图所示,在离水面高度5米的岸上有人用绳子拉船靠岸,开始时绳子BC的长度为13米,此人以每秒0.5米的速度收绳.问:
(1)未开始收绳的时候,图中船B距岸A的长度AB是多少米?
(2)收绳10秒后船向岸边移动了多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是以AB为直径的⊙O上一动点,过点C作⊙O直径CD,过点B作BE⊥CD于点E.已知AB=6cm,设弦AC的长为xcm,B,E两点间的距离为ycm(当点C与点A或点B重合时,y的值为0).
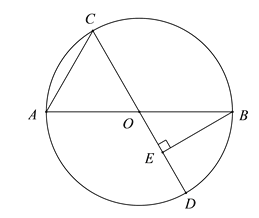
小冬根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小冬的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
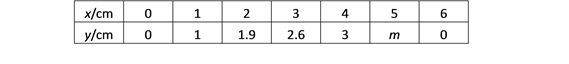
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)在(2)的条件下,当函数图象与直线![]() 相交时(原点除外),∠BAC的度数是_____.
相交时(原点除外),∠BAC的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
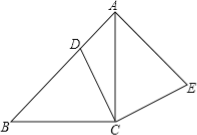
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点, 则该三角形被剖分的网格中的结点个数和线段数分别是多少呢?
问题探究:要研究上面的问题,我们不妨先从特例入手,进而找到一般规律
探究一:将一个边长为2的正三角形的三条边平分,连接各边中点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
如图1,连接边长为2的正三角形三条边的中点,从上往下:共有1+2+3=6个结点.边长为1的正三角形,第一层有1个,第二层有2个,共有1+2=3个,线段数为3×3=9条;边长为2的正三角形有1个,线段数为3条,总共有3×(1+2+1)=2×(1+2+3)=12条线段.

探究二:将一个边长为3的正三角形的三条边三等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
如图2,连接边长为3的正三角形三条边的对应三等分点,从上往下:共有1+2+3+4=10个结点.边长为1的正三角形,第一层有1个,第二层有2个,第三层有3个,共有1+2+3=6个,线段数为3×6=18条;边长为2的正三角形有1+2=3个,线段数为3×3=9条,边长为3的正三角形有1个,线段数为3条,总共有3×(1+2+3+1+2+1)=3×(1+2+3+4)=30条线段.
探究三:
请你仿照上面的方法,探究将边长为4的正三角形的三条边四等分(图3),连接各边对应的等分点,该三角形被剖分的网格中的结点个数和线段数分别是多少?
(画出示意图,并写出探究过程)
问题解决:
请你仿照上面的方法,探究将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?(写出探究过程)
实际应用:
将一个边长为30的正三角形的三条边三十等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2+(2m﹣1)x﹣2m.
(1)若m=1,抛物线C交x轴于A,B两点,求AB的长;
(2)若一次函数y=kx+mk的图象与抛物线C有唯一公共点,求m的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市为方便行人过马路,打算修建一座高为4x(m)的过街天桥.已知天桥的斜面坡度i=1:0.75是指坡面的铅直高度DE(CF)与水平宽度AE(BF)的比,其中DC∥AB,CD=8x(m).
(1)请求出天桥总长和马路宽度AB的比;
(2)若某人从A地出发,横过马路直行(A→E→F→B)到达B地,平均速度是2.5m/s;返回时从天桥由BC→CD→DA到达A地,平均速度是1.5m/s,结果比去时多用了12.8s,请求出马路宽度AB的长.
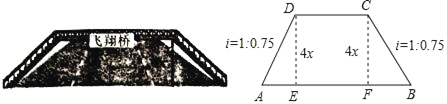
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com