
 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )| A. | ($\frac{\sqrt{3}}{2}$)2016 | B. | ($\sqrt{3}$)2016 | C. | 22017 | D. | ($\sqrt{3}$)2017 |
分析 根据已知和菱形的性质可分别求得AC,AC1,AC2的长,从而可发现规律根据规律不难求得第n个菱形的边长.
解答 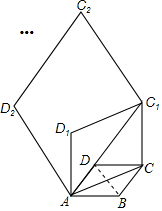 解:连接DB,
解:连接DB,
∵四边形ABCD是菱形,
∴AD=AB.AC⊥DB,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴DB=AD=1,
∴BM=$\frac{1}{2}$,
∴AM=$\frac{\sqrt{3}}{2}$,
∴AC=$\sqrt{3}$,
同理可得AC1=$\sqrt{3}$AC=($\sqrt{3}$)2,AC2=$\sqrt{3}$AC1=3$\sqrt{3}$=($\sqrt{3}$)3,
按此规律所作的第n个菱形的边长为( $\sqrt{3}$)n-1,
则第2017个菱形的边长为( $\sqrt{3}$)2016,
故选:B.
点评 此题主要考查菱形的性质、等边三角形的判定和性质以及学生探索规律的能力.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
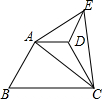 如图,将梯形ABCD沿直线AC翻折,点B落在点E处,联结ED,如果∠B=60°,∠ACB=40°,ED∥AB,那么∠AED的度数为20°.
如图,将梯形ABCD沿直线AC翻折,点B落在点E处,联结ED,如果∠B=60°,∠ACB=40°,ED∥AB,那么∠AED的度数为20°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
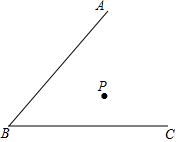 如图,已知点P为∠ABC内一点,利用直尺和圆规确定一条过点P的直线,分别交AB,BC于点E,F,使得BE=BF,(不写作法,保留作图痕迹)
如图,已知点P为∠ABC内一点,利用直尺和圆规确定一条过点P的直线,分别交AB,BC于点E,F,使得BE=BF,(不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
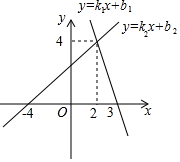 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为( )
如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com