
【题目】根据要求,解答下列问题:
(1)解答下列问题 ①方程x2﹣2x+1=0的解为;
②方程x2﹣3x+2=0的解为;
③方程x2﹣4x+3=0的解为;
…
(2)根据以上方程特征及其解的特征,请猜想: ①方程x2﹣9x+8=0的解为;
②关于x的方程的解为x1=1,x2=n.
(3)请用配方法解方程x2﹣9x+8=0,以验证猜想结论的正确性.
【答案】
(1)x1=x2=1;x1=1,x2=2;x1=1,x2=3
(2)1、8;x2﹣(1+n)x+n=0
(3)x-9x=-8
x-9x+ ![]() =-8+
=-8+ ![]()
(x- ![]() )=
)= ![]()
x- ![]() =
= ![]()
![]()
所以 ![]()
所以猜想正确。
【解析】解:(1)①(x﹣1)2=0,解得x1=x2=1,即方程x2﹣2x+1=0的解为x1=x2=1,; ②(x﹣1)(x﹣2)=0,解得x1=1,x2=2,所以方程x2﹣3x+2=0的解为x1=1,x2=2,;
③(x﹣1)(x﹣3)=0,解得x1=1,x2=3,方程x2﹣4x+3=0的解为x1=1,x2=3;
…
2)根据以上方程特征及其解的特征,请猜想:
①方程x2﹣9x+8=0的解为x1=1,x2=8;
②关于x的方程x2﹣(1+n)x+n=0的解为x1=1,x2=n.
【考点精析】解答此题的关键在于理解配方法的相关知识,掌握左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题,以及对因式分解法的理解,了解已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势.


科目:初中数学 来源: 题型:
【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,他这天下午行驶里程如下:(单位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他将最后一名乘客送到目的地时,距下午出车地点是多少千米?
(2)若汽车耗油量为![]() 升∕千米,这天下午共耗油多少升
升∕千米,这天下午共耗油多少升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①已知正方形ABCD的边BC、CD上分别有E、F两点,且∠EAF=45°,现将△ADF绕点A顺时针旋转90°至△ABH处.
(1)线段EF、BE、DF有何数量关系?并说明理由;
模仿(1)中的方法解决(2)、(3)两个问题:
(2)如图②,若将E、F移至BD上,其余条件不变,且BE=![]() ,DF=3,求EF的长;
,DF=3,求EF的长;
(3)如图③,图形变成矩形ABCD,∠EAF=45°,BE=3,AB=6,AD=10,求DF和EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( ) 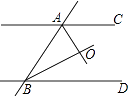
A.∠BAO与∠CAO相等
B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余
D.∠ABO与∠DBO不等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C.
(Ⅰ)求直线y=kx+b的函数解析式;
(Ⅱ)若点P(x,y)是抛物线y=﹣x2+2x+1上的任意一点,设点P到直线AB的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;
(Ⅲ)若点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(![]() ,
, ![]() )、Q(
)、Q(![]() ,
, ![]() )是该反比例函数图象上的两点,且
)是该反比例函数图象上的两点,且![]() 时,
时, ![]() ,指出点P、Q各位于哪个象限?并简要说明理由.
,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2 017次后形成的图形中所有正方形的面积和是( )
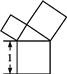

图1 图2
A. 2015 B. 2016 C. 2017 D. 2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com