
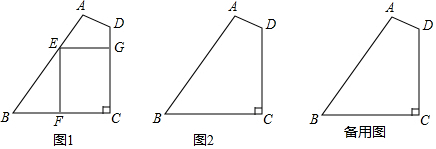
分析 (1)由平行线的性质得出∠CGE=90°,同理:∠CFE=90°,进而得出四边形EFCG是矩形;
(2)根据矩形的性质和正方形的性质即可画出图形;
(3)先判断出四边形EFCG面积最大时,此四边形为正方形,进而用含30°的直角三角形的性质和等腰直角三角形的性质求解即可.
解答 解:(1)∵EG∥BC,
∴∠C+∠CGE=180°,
∵∠C=90°,
∴∠CGE=90°,
同理:∠CFE=90°,
∴∠CGE=∠CFE=∠C=90°,
∴四边形EFCG是矩形,
(2)四边形EFCG可以是正方形,
理由:如图,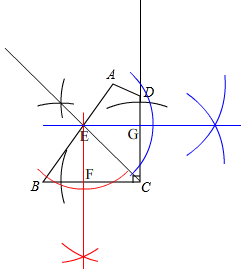 先作出∠BCD的平分线,与AB相交于点E,再过点E作EF⊥BC,EG⊥CD,得出的四边形EFCG是正方形,
先作出∠BCD的平分线,与AB相交于点E,再过点E作EF⊥BC,EG⊥CD,得出的四边形EFCG是正方形,
证明:∵EF⊥BC,EG⊥CD,
∴∠CFE=∠CGE=90°,
∵∠BCD=90°,
∴∠CGE=∠CFE=∠C=90°,
∴四边形EFCG是矩形,
∵CE平分∠BCD,
∴∠BCE=$\frac{1}{2}$∠BCD=45°,
∴∠CEF=∠BCE=45°,
∴CF=EF,
∵四边形EFCG是矩形,
∴矩形EFCG是正方形.
(3)∵S矩形EFCG=$\frac{1}{2}$CF×CG,
∴当CF=CG时,矩形EFCG的面积最大,
如图,在Rt△BEF中,∠B=60°,
∴BE=2BF,EF=$\sqrt{3}$BF,
在Rt△CEF中,∠ECF=45°,
∴CF=EF=$\sqrt{3}$BF,
∵BC=BF+CF=BF+$\sqrt{3}$BF=6,
∴BF=3($\sqrt{3}$-1),
∴BE=2BF=6($\sqrt{3}$-1).
即:BE=6($\sqrt{3}$-1)时,四边形EFCG的面积最大.
点评 此题是四边形综合题,主要考查了矩形的判定和性质,正方形的性质和判定,基本作图,解本题的关键是画出图形,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
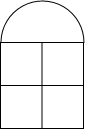 如图,是一扇窗户的设计图,它由四个小正方形及一个半圆组成,已知半圆的半径为a米.(结果保留π)
如图,是一扇窗户的设计图,它由四个小正方形及一个半圆组成,已知半圆的半径为a米.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
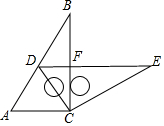 如图,两个含有30°角且大小相同的三角板(Rt△ABC和Rt△DCE)摆放在一起,直角顶点重合,点D刚好落在AB边上.
如图,两个含有30°角且大小相同的三角板(Rt△ABC和Rt△DCE)摆放在一起,直角顶点重合,点D刚好落在AB边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
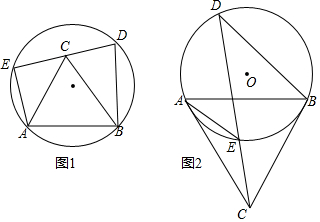
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com