
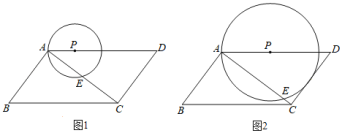
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)线段AC的长度是 .
(2)如图2,当⊙P与边CD相切于点F时,求AP的长;
(3)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .
【答案】(1)8;(2)AP=![]() ;(3)
;(3)![]() <AP<
<AP<![]() 或AP=5.
或AP=5.
【解析】
(1)在Rt△ABC中,直接利用勾股定理求解即可;
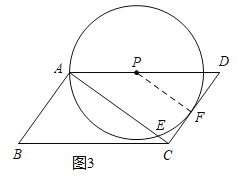
(2)连接PF,如图3,利用平行四边形的性质和切线的性质可得PF∥AC,进而可证明△DPF∽△DAC,然后根据相似三角形的性质列比例式求解即得AP的长;
(3)先利用平行四边形的面积求出当⊙P与BC相切时圆的半径,可发现此时⊙P与平行四边形ABCD的边有5个公共点;再分两种情况:①⊙P与边AD、CD分别有两个公共点;②⊙P过点A、C、D三点,分别求出即可得到答案.
解:(1)∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC=![]() ,
,
故答案为:8;
(2)如图3所示,连接PF,设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴![]() ,即
,即![]() ,
,
解得:x=![]() ,
,
即AP=![]() ;
;
(3)当⊙P与BC相切时,设切点为G,连接PG,如图4,则SABCD=![]() ×6×8×2=10PG,解得:PG=
×6×8×2=10PG,解得:PG=![]() ,此时⊙P与平行四边形ABCD的边的公共点的个数为5;
,此时⊙P与平行四边形ABCD的边的公共点的个数为5;
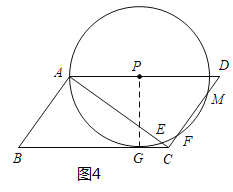
①当⊙P与边AD、CD分别有两个公共点,与BC没有公共点时,![]() <AP<
<AP<![]() ,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
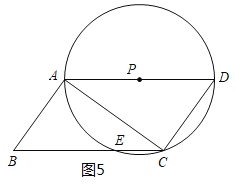
②当⊙P过点A、C、D三点,如图5,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:![]() <AP<
<AP<![]() 或AP=5,
或AP=5,
故答案为:![]() <AP<
<AP<![]() 或AP=5.
或AP=5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
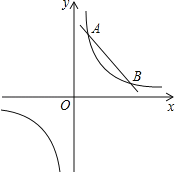
【题目】如图,直线y=﹣x+b与反比例函数y=![]() 的图形交于A(a,4)和B(4,1)两点
的图形交于A(a,4)和B(4,1)两点
(1)求b,k的值;
(2)若点C(x,y)也在反比例函数y=![]() (x>0)的图象上,求当2≤x≤6时,函数值y的取值范围;
(x>0)的图象上,求当2≤x≤6时,函数值y的取值范围;
(3)将直线y=﹣x+b向下平移m个单位,当直线与双曲线没有交点时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
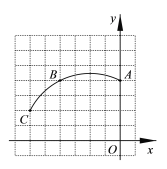
(1)利用网格图确定该圆弧所在圆的圆心D的位置(保留画图痕迹);
(2)连接AD、CD,则⊙D的半径为_ __(结果保留根号),∠ADC的度数为_ __;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
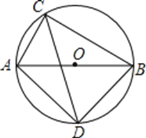
【题目】如图,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D.
(1)求BD的长;
(2)将△ADC绕D点顺时针方向旋转90°,请补充旋转后图形,并计算CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于点A(﹣2,0),点B(1,0),交y轴于点C(0,2).
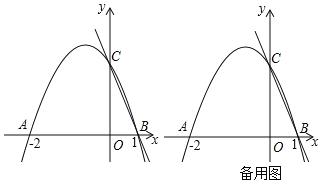
(1)求二次函数的解析式;
(2)连接AC,在直线AC上方的抛物线上有一点N,过点N作y轴的平行线,交直线AC于点F,设点N的横坐标为n,线段NF的长为l,求l关于n的函数关系式;
(3)若点M在x轴上,是否存在点M,使以B、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
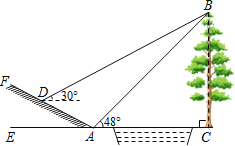
【题目】如图所示,某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:![]() ,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() 取1.73.
取1.73.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师和同学们做一个游戏:他在三张硬纸片上分别写出一个代数式,背面分别标上序号①、②、③,摆成如图所示的一个等式,然后翻开纸片②是4x2+5x+6,翻开纸片③是3x2﹣x﹣2.
![]()
解答下列问题
(1)求纸片①上的代数式;
(2)若x是方程2x=﹣x﹣9的解,求纸片①上代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】时代天街某商场经营的某品牌书包,6月份的销售额为20000元,7月份因为厂家提高了出厂价,商场把该品牌书包售价上涨20%,结果销量减少50个,使得销售额减少了2000元.
(1)求6月份该品牌书包的销售单价;
(2)若6月份销售该品牌书包获利8000元,8月份商场为迎接中小学开学做促销活动,该书包在6月售价的基础上一律打八折销售,若成本上涨5%,则销量至少为多少个,才能保证8月份的利润比6月份的利润至少增长6.25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
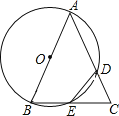
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com