
已知正方形OABC中,O为坐标原点,点A在y轴的正半轴上,点C在x轴的正半轴上,点B(4,4).二次函数y=-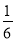 x2+bx+c的图象经过点A、B.点P(t,0)是x轴上一动点,连接AP.
x2+bx+c的图象经过点A、B.点P(t,0)是x轴上一动点,连接AP.
(1)求此二次函数的解析式;
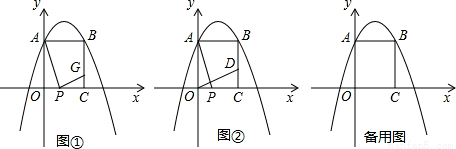
(2)如图①,过点P作AP的垂线与线段BC交于点G,当点P在线段OC(点P不与点C、O重合)上运动至何处时,线段GC的长有最大值,求出这个最大值;
(3)如图②,过点O作AP的垂线与直线BC交于点D,二次函数y=-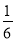 x2+bx+c的图象上是否存在点Q,使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形?若存在,求出t的值;若不存在,请说明理由.
x2+bx+c的图象上是否存在点Q,使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形?若存在,求出t的值;若不存在,请说明理由.
(1) 二次函数解析式为y=- x2+
x2+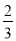 x+4;(2) P(2,0)时,GC的最大值是1;(3) 存在点Q(-6,-6)或(6,2),使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形.
x+4;(2) P(2,0)时,GC的最大值是1;(3) 存在点Q(-6,-6)或(6,2),使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形.
【解析】
试题分析:(1)根据正方形的性质求出点A的坐标,然后把点A、B的坐标代入函数解析式求出b、c,即可得解;
(2)表示出PO、PC,再根据同角的余角相等求出∠OAP=∠CPG,然后求出△AOP和△PCG相似,再根据相似三角形对应边成比例列式表示出GC,然后根据二次函数的最值问题解答;
(3)求出∠OAP=∠COD,再利用“角边角”证明△AOP和△OCD全等,根据全等三角形对应边相等可得OP=CD,再求出PC,从而得到点D的坐标,然后分①点Q在直线BC的右边时,根据平行四边形的对边平行且相等表示出点Q的坐标,再代入二次函数解析式计算即可求出t值,②点Q在直线BC的左边时,根据平行四边形的对边平行且相等表示出点Q的坐标,再代入二次函数解析式计算即可求出t值.
试题解析:(1)∵B(4,4),
∴AB=BC=4,
∵四边形ABCD是正方形,
∴OA=4,
∴A(0,4),
将点A(0,4),B(4,4)代入y=- x2+bx+c得
x2+bx+c得
 ,
,
解得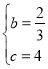 .
.
∴二次函数解析式为y=- x2+
x2+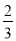 x+4;
x+4;
(2)∵P(t,0),
∴OP=t,PC=4-t,
∵AP⊥PG,
∴∠APO+∠CPG=180°-90°=90°,
∵∠OAP+∠APO=90°,
∴∠OAP=∠CPG,
又∵∠AOP=∠PCG=90°,
∴△AOP∽△PCG,
∴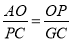 ,
,
即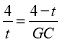 ,
,
整理得,GC=-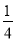 (t-2)2+1,
(t-2)2+1,
∴当t=2时,GC有最大值是1,
即P(2,0)时,GC的最大值是1;
(3)存在点Q,使得以P、C、Q、DP、C、Q、DP、C、Q、D为顶点的四边形是以PC为边的平行四边形.
理由如下:如图1、2,易得∠OAP=∠COD,
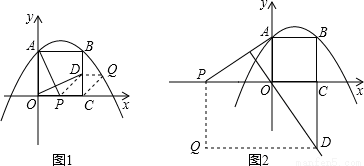
在△AOP和△OCD中,
 ,
,
∴△AOP≌△OCD(ASA),
∴OP=CD,
由P、C、Q、DP、C、Q、DP、C、Q、D为顶点的四边形是以PC为边的平行四边形得,PC∥DQ且PC=DQ,
∵P(t,0),D(4,t),
∴PC=DQ=|t-4|,
∴点Q的坐标为(t,t)或(8-t,t),
①当Q(t,t)时,-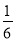 t2+
t2+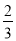 t+4=t,
t+4=t,
整理得,t2+t-24=0,
解得t1=4(舍去),t2=-6,
②当Q(8-t,t)时,-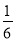 (8-t)2+
(8-t)2+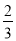 (8-t)+4=t,
(8-t)+4=t,
整理得,t2-6t+8=0,
解得t1=2,t2=4(舍去),
综上所述,存在点Q(-6,-6)或(6,2),使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形.
考点:二次函数综合题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源:2014-2015学年山东省滨州市九年级上学期期末考试数学试卷(解析版) 题型:填空题
已知关于x的一元二次方程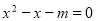 有两个不相等的实数根,则实数m的取值范围是 .
有两个不相等的实数根,则实数m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:选择题
下列方程是一元二次方程的是 ( )
A.x2-6x+2 B.2x2-y+1=0 C.x2=0 D.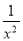 + x=2
+ x=2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:填空题
已知关于x的一元二次方程x2+3x-a=0的一个根是2,则字母a的值为_____________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:选择题
如图,CD是⊙O的直径,弦DE∥OA,若∠D的度数是50°,则∠A的度数是 ( )
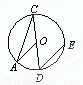
A.25° B.30° C.40° D.50°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:解答题
一个两位数的两个数字之和为9,把这个两位数的个位数字与十位数字互换得到一个新的两位数,他与原两位数的积为1458,求原两位数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:填空题
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
若A(m,y1),B(m+1,y2)两点都在该函数的图象上,当m= 时,y1=y2.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分12分)
【问题背景】
已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.
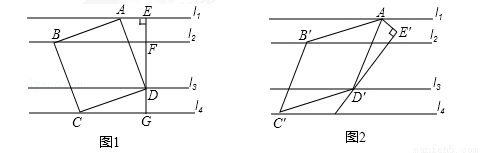
【问题探究】
(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为_ _.
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.
【问题拓展】
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:填空题
已知α、β方程x2+2x-5=0的两根,则α2+αβ+3α+β的值是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com