
【题目】如图,在平面直角坐标系中,直线AB和抛物线交于点A(﹣4,0),B(0,4),且点B是抛物线的顶点.
(1)求直线AB和抛物线的解析式.
(2)点P是直线上方抛物线上的一点,求当△PAB面积最大时点P的坐标.
(3)M是直线AB上一动点,在平面直角坐标系内是否存在点N,使以O、B、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】
(1)
答案
解:设直线的解析式为y=kx+b.
∵将A(﹣4,0),B(0,4)代入得: ![]() ,解得k=1,b=4,
,解得k=1,b=4,
∴直线AB的解析式为y=x+4.
设物线的解析式为y=ax2+4.
∵将A(﹣4,0)代入得:16a+4=0,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+4.
x2+4.
;
答案
解:设直线的解析式为y=kx+b.
∵将A(﹣4,0),B(0,4)代入得: ![]() ,解得k=1,b=4,
,解得k=1,b=4,
∴直线AB的解析式为y=x+4.
设物线的解析式为y=ax2+4.
∵将A(﹣4,0)代入得:16a+4=0,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+4.
x2+4.
;答案;
解:设直线的解析式为y=kx+b.
∵将A(﹣4,0),B(0,4)代入得: ![]() ,解得k=1,b=4,
,解得k=1,b=4,
∴直线AB的解析式为y=x+4.
设物线的解析式为y=ax2+4.
∵将A(﹣4,0)代入得:16a+4=0,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+4.
x2+4.
(2)
解:如图1所示,过点P作PQ⊥x轴,交AB于点Q.

设点P的坐标为(a,﹣ ![]() +4),则点Q的坐标为(a,a+4).则PQ=﹣
+4),则点Q的坐标为(a,a+4).则PQ=﹣ ![]() +4﹣(a+4)=﹣
+4﹣(a+4)=﹣ ![]() ﹣a.
﹣a.
∵S△ABP的面积= ![]() PQ(xB﹣xA)=
PQ(xB﹣xA)= ![]() ×4×(﹣
×4×(﹣ ![]() ﹣a)=﹣
﹣a)=﹣ ![]() a2﹣2a=﹣
a2﹣2a=﹣ ![]() (a+2)2+2,
(a+2)2+2,
∴当a=﹣2时△ABP的面积最大,此时P(﹣2,2).
(3)
解:如图2所示:延长MN交x轴与点C.
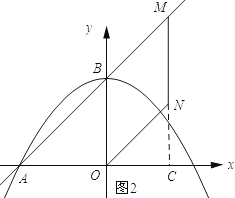
∵MN∥OB,OB⊥OC,
∴MN⊥OC.
∵OA=OB,∠AOB=90°,
∴∠BA0=45°.
∵ON∥AB,
∴∠NOC=45°.
∴OC=ON× ![]() =4×
=4× ![]() =2
=2 ![]() ,NC=ON×
,NC=ON× ![]() =4×
=4× ![]() =2
=2 ![]() .
.
∴点N的坐标为(2 ![]() ,2
,2 ![]() ).
).
如图3所示:过点N作NC⊥y轴,垂足为C.
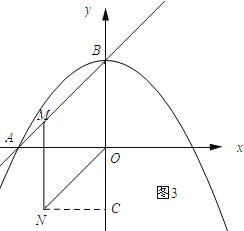
∵OA=OB,∠AOB=90°,
∴∠OBA=45°.
∵ON∥AB,
∴∠NOC=45°.
∴OC=ON× ![]() =4×
=4× ![]() =2
=2 ![]() ,NC=ON×
,NC=ON× ![]() =4×
=4× ![]() =2
=2 ![]() .
.
∴点N的坐标为(﹣2 ![]() ,﹣2
,﹣2 ![]() ).
).
如图4所示:连接MN交y轴与点C.
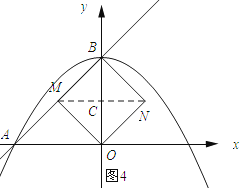
∵四边形BNOM为菱形,OB=4,
∴BC=OC=2,MC=CN,MN⊥OB.
∴点的纵坐标为2.
∵将y=2代入y=x+4得:x+4=2,解得:x=﹣2,
∴点M的坐标为(﹣2,2).
∴点N的坐标为(2,2).
如图5所示:

∵四边形OBNM为菱形,
∴∠NBM=∠ABO=45°.
∴四边形OBNM为正方形.
∴点N的坐标为(﹣4,4).
综上所述点N的坐标为 ![]() 或
或 ![]() 或(﹣4,4)或(2,2)
或(﹣4,4)或(2,2)
【解析】(1)设直线的解析式为y=kx+b,将A(﹣4,0),B(0,4)代入得到关于k、b的方程组,然后解得k、b的值即可;设抛物线的解析式为y=ax2+4,然后将点A的坐标代入求得a的值即可;(2)过点P作PQ⊥x轴,交AB于点Q.设点P(a,﹣ ![]() +4),Q(a,a+4).则PQ=﹣
+4),Q(a,a+4).则PQ=﹣ ![]() ﹣a,然后依据三角形的面积公式列出△ABP的面积与a的函数关系式,然后依据二次函数的性质求解即可;(3)先根据题意画出图形,需要注意本题共有4种情况,然后依据菱形的性质、等腰直角三角形的性质以及特殊锐角三角函数值求解即可.
﹣a,然后依据三角形的面积公式列出△ABP的面积与a的函数关系式,然后依据二次函数的性质求解即可;(3)先根据题意画出图形,需要注意本题共有4种情况,然后依据菱形的性质、等腰直角三角形的性质以及特殊锐角三角函数值求解即可.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ ![]() ,tan48°≈
,tan48°≈ ![]() ,sin64°≈
,sin64°≈ ![]() ,tan64°≈2)
,tan64°≈2)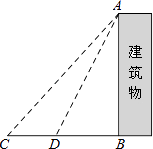
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.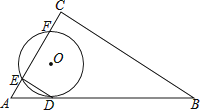
(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 ![]() (k≠0)的图象过点A(﹣3,2).
(k≠0)的图象过点A(﹣3,2).
(1)求这个反比例函数的解析式;
(2)若B(x1 , y1),C(x2 , y2),D(x3 , y3)是这个反比例函数图象上的三个点,若x1>x2>0>x3 , 请比较y1 , y2 , y3的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?(参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)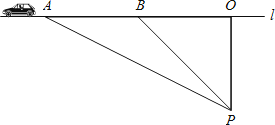
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 ![]() 的一部分.请根据图中信息解析下列问题:
的一部分.请根据图中信息解析下列问题:
(1)求y与x的函数关系式;
(2)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点. 
(1)求证:CF为⊙O的切线;
(2)若⊙O的半径为 ![]() cm,弦BD的长为3cm,求CF的长.
cm,弦BD的长为3cm,求CF的长. 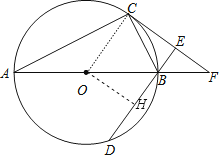
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( ) 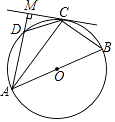
A.20°
B.35°
C.40°
D.55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com