Question

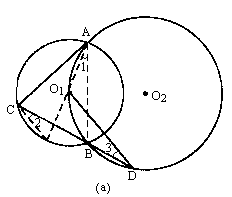
如图(a)、(b)、(c)，⊙O₁与⊙O₂交于A、B两点，点O₁在⊙O₂上，C为⊙O₁中优弧上任意一点，直线CB交⊙O₂于D，连结O₁D．

(1)用两种不同的方法证明：DO₁⊥AC；

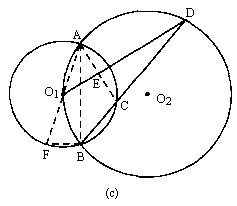
(2)若点C在劣弧上，(1)中的结论是否仍成立？请在图(c)中画出图形，并证明你的结论．

Answer 1

答案：
解析：

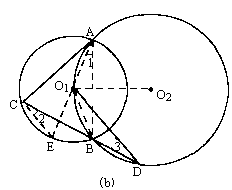
(1)证明：[证法一] 　　如图(a)，连结AB，连结AO1并延长交⊙O1于E，连结CE．则 　　∠1＝∠2，∠1＝∠3， 　　∴∠2＝∠3，∴CE∥O1D． 　　∵AE是⊙O1的直径，∴CE⊥AC． 　　∴DO1⊥AC． 　　[证法二] 　　如图(b)，连结AO1、AB、O1O2、BO1，则AB⊥O1O2． 　　∵∠O1AB＝∠D， 　　∠AO1O2＝∠AO1B＝∠C， 　　∴∠C＋∠D＝∠AO1O2＋∠O1AB 　　＝． 　　∴O1D⊥AC． 　　(2)如图(c)，当C点在劣弧上时，(1)中的结论仍成立，即DO1⊥AC． 　　证明：连结AB，连结AO1并延长交⊙O1于F，连结FB．连结AC交DO1于E． 　　∵四边形AFBC内接于⊙O1， 　　∴∠F＝∠ACD． 　　∵AF是⊙O1的直径， 　　∴∠ABF＝． 　　∴∠FAB＋∠F＝． 　　又∵∠FAB＝∠D， 　　∴∠D＋∠ACD＝． 　　∴∠DEC＝． 　　∴DO1⊥AC．

提示：

(1)连结相交两圆的公共弦AB，当一个圆过另一个圆的圆心时，要研究以O1为角顶点的圆心角和圆周角；(2)一般来讲，图形变化证明方法不发生变化．