
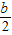 ,0),点B坐标(0,b),
,0),点B坐标(0,b),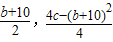 ),
), ,0),点B坐标(0,b),
,0),点B坐标(0,b),
 |,OB=|b|,
|,OB=|b|,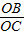 =
=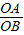
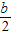 |,
|,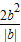
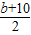 且抛物线对称轴过点C,
且抛物线对称轴过点C,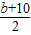 |=
|=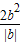 .
.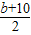 =-2b,
=-2b, (舍去)
(舍去)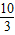 不合题意,舍去.
不合题意,舍去.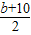 =-2b,
=-2b,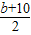 =2b,
=2b,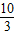 ,
,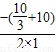 =
= >0,
>0,

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《图形的相似》(04)(解析版) 题型:解答题
 cm的速度向B点方向运动,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与边AB相交于E、F两点.过E作EG⊥DE交射线BC于G.
cm的速度向B点方向运动,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与边AB相交于E、F两点.过E作EG⊥DE交射线BC于G.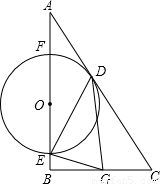
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
 cm的速度向B点方向运动,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与边AB相交于E、F两点.过E作EG⊥DE交射线BC于G.
cm的速度向B点方向运动,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与边AB相交于E、F两点.过E作EG⊥DE交射线BC于G.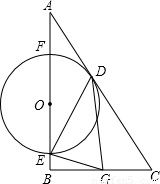
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com