
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
(1)∠BAE的度数;
(2)∠DAE的度数;
【答案】
(1)解:∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°,
∵AE平分∠BAC,
∴∠BAE=1/2∠BAC=40°
(2)解:∵AD⊥BC,
∴∠ADE=90°,
而∠ADE=∠B+∠BAD,
∴∠BAD=90°-∠B=90°-70°=20°,
∴∠DAE=∠BAE-∠BAD=40°-20°=20°
【解析】根据三角形内角和定理得∠BAC=180°-∠B-∠C=80°,然后根据角平分线定义得∠BAE=![]() ∠BAC=40°;
∠BAC=40°;
由于AD⊥BC,则∠ADE=90°,根据三角形外角性质得∠ADE=∠B+∠BAD,所以∠BAD=90°-∠B=20°,然后利用∠DAE=∠BAE-∠BAD进行计算;


科目:初中数学 来源: 题型:
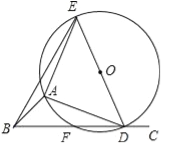
【题目】如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A、D分别再∠ABC的两边BA、BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.
(1)直接写出∠AFE的度数;
(2)当点D在点F的右侧时,①求证:EF﹣DF=![]() AF;
AF;
②若AB=![]() ,
,![]() <BE≤
<BE≤![]() ,求⊙O的面积S的取值范围.
,求⊙O的面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.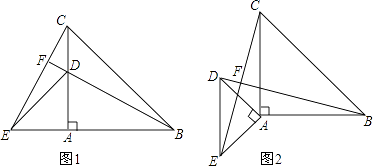
(1)试判断BD、CE的数量关系,并说明理由;
(2)延长BD交CE于点F,试求∠BFC的度数;
(3)把两个等腰直角三角形按如图2放置,(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:![]() 交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( ) 
A.45°
B.54°
C.40°
D.50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com