

分析 (1)由x张用A方法,就有(19-x)张用B方法,就可以分别表示出侧面个数和底面个数;
(2)由侧面个数和底面个数比为3:2建立方程求出x的值,求出侧面的总数就可以求出结论.
解答 解:(1)∵裁剪时x张用A方法,
∴裁剪时(19-x)张用B方法.
∴侧面的个数为:6x+4(19-x)=(2x+76)个,
底面的个数为:5(19-x)=(95-5x)个;
(2)由题意,得(2x+76):(95-5x)=3:2,
解得:x=7,
∴盒子的个数为:$\frac{2×7+76}{3}$=30.
答:裁剪出的侧面和底面恰好全部用完,能做30个盒子.
点评 本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,列代数式的运用以及分式方程的应用,解答时根据裁剪出的侧面和底面个数相等建立方程是关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:选择题
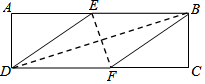 在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE,现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )
在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE,现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )| A. | ①是假命题,②是假命题 | B. | ①是真命题,②是假命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①是真命题,②是真命题 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,2,$\sqrt{3}$ | B. | 3,4,5 | C. | 1,1,$\sqrt{2}$ | D. | 6,12,13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com