
 小明在楼高AB=15米的楼顶A处测得一电视塔底部C的俯角为31°,测得塔高D的仰角为52°,求楼顶A对塔顶D的距离(结果保留整数)(参考数据:sin31°=0.52,cos 31°=0.86,tan 31°=0.80,sin52°=0.79,cos 52°═0.62,tan52°=1.28)
小明在楼高AB=15米的楼顶A处测得一电视塔底部C的俯角为31°,测得塔高D的仰角为52°,求楼顶A对塔顶D的距离(结果保留整数)(参考数据:sin31°=0.52,cos 31°=0.86,tan 31°=0.80,sin52°=0.79,cos 52°═0.62,tan52°=1.28) 分析 作AE⊥CD于点E.则CE=AB,在直角△ACE中利用正切函数求得AE的长,然后在直角△ADE中利用余弦函数求得AD的长.
解答 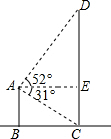 解:作AE⊥CD于点E.则CE=AB=15(米).
解:作AE⊥CD于点E.则CE=AB=15(米).
∵在直角△ACE中,tan∠EAC=$\frac{CE}{AE}$,
∴AE=$\frac{CE}{tan∠EAC}$=$\frac{15}{0.80}$=18.75(米).
∵直角△ADE中,cos∠DAE=$\frac{AE}{AD}$,
∴AD=$\frac{AE}{cos52°}$=$\frac{18.75}{0.62}$≈30(米).
答:楼顶A对塔顶D的距离是30米.
点评 本题考查了仰角和俯角的应用,决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形EBCF中,点A为EF的中点,AB=AC,∠BAC=90°,BE=4$\sqrt{2}$,CF=5$\sqrt{2}$,EF=6,求△ABE的面积.
如图,在四边形EBCF中,点A为EF的中点,AB=AC,∠BAC=90°,BE=4$\sqrt{2}$,CF=5$\sqrt{2}$,EF=6,求△ABE的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com