设k为实数,关于x的一元二次方程x2+kx+k+1=0的两个实根分别为x1,x2,若x1+2x22=k,则k=________.
5
分析:k为实数,关于x的一元二次方程x2+kx+k+1=0的两个实根分别为x1,x2,根据根与系数的关系列出关于k的等式即可得出答案.
解答:∵x的一元二次方程x2+kx+k+1=0的两个实根分别为x1、x2,
∴x22+kx2+k+1=0,
∴x22=-(kx2+k+1)①
根据韦达定理:
x1+x2=-k ②
x1x2=k+1 ③
∵x22=x22+x1x2-x1x2,
=(x1+x2)x2-x1x2
=-kx2-k-1,
∴x1+2x22=k,
x1+2(-kx2-k-1)=k,
x1+x2-x2-2kx2-2k-2=k,
-k-x2-2kx2-2k-2=k,
x2+2kx2+4k+2=0,
即 (2k+1)(2+x2)=0
∴k=-0.5或x2=-2
∵k=-0.5时,
△=(-0.5)2-4×1×(-0.5+1)
=0.25-2
=-1.75<0,
∴x2=-2,
把x2=-2代入原方程x2+kx+k+1=0,得
4-2k+k+1=0,
解得k=5,
检验:△=52-4×1×(5+1)=1>0,
∴k=5.
点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.



 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案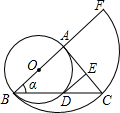 已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,DE切⊙O于D,交AC于E.
已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,DE切⊙O于D,交AC于E.