
【题目】如图,已知![]() 分别是
分别是![]() 的内角平分线,过
的内角平分线,过![]() 点作
点作![]() ;
;![]() 垂足分别为
垂足分别为![]() 连结
连结![]() 若
若![]() 则
则![]() 的长等于_______(用含
的长等于_______(用含![]() 的代数式表示结果).
的代数式表示结果).

【答案】![]() (
(![]() )
)
【解析】
延长AG交BC于N,延长AF交BC于M,根据AF⊥BD,AG⊥CE,求证Rt△AGC≌Rt△NGC,可得AC=CN,AG=NG,同理可证:AF=FM,AB=BM.然后得出GF是△AMN的中位线,利用AB+AC=MB+CN=BN+MN+CM+MN,BC=BN+MN+CM,利用等量代换即可.
延长AG交BC于N,延长AF交BC于M.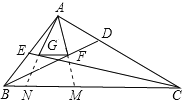
∵AF⊥BD,AG⊥CE,
∴∠AGC=∠CGN=90°,∠AFB=∠BFM=90°,
在Rt△AGC和Rt△NGC中,
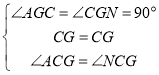 ,
,
∴△AGC≌Rt△NGC,
∴AC=CN,AG=NG,
同理可证:AF=FM,AB=BM,
∴GF是△AMN的中位线
∴GF=![]() MN,
MN,
∵AB+AC=MB+CN=BN+MN+CM+MN,而BC=BN+MN+CM,
∴AB+AC-BC=MN,
∴GF=![]() MN
MN![]() (AB+AC-BC);即FG
(AB+AC-BC);即FG![]() (
(![]() )
)
故答案为:![]() (
(![]() ) .
) .


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )

A. 7 B. 8 C. 12 D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=60°,CE为△ABC的角平分线,AC边上的高BD与CE所在的直线交于点F,若∠ABD:∠ACF=2:3,则∠BEC的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
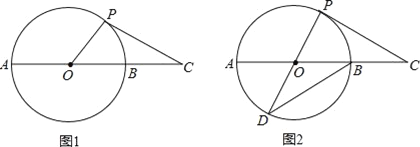
【题目】如图1,延长⊙O的直径AB至点C,使得BC=![]() AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
(1)∠C的最大度数为 ;
(2)当⊙O的半径为3时,△OPC的面积有没有最大值?若有,说明原因并求出最大值;若没有,请说明理由;
(3)如图2,延长PO交⊙O于点D,连结DB,当CP=DB时,求证:CP是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线![]() 过点D,B,C三点.
过点D,B,C三点.

(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线![]() 上吗?请说明理由;
上吗?请说明理由;
(4)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 的边
的边![]() 平行于
平行于![]() 轴,
轴,![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第四象限,点
在第四象限,点![]() 是
是![]() 边上的一个动点.
边上的一个动点.

(1)若点![]() 在边
在边![]() 上,
上,![]() 求点
求点![]() 的坐标;
的坐标;
(2)若点![]() 在边
在边![]() 或
或![]() 上,点
上,点![]() 是
是![]() 与
与![]() 轴的交点如图2,过点
轴的交点如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 过点
过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 它们相交于点
它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标.(直接写出答案)
的坐标.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
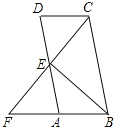
【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=100°,求∠ABE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com