
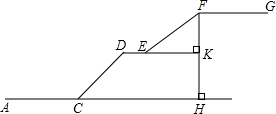
 ��ͼ��У������ʯ���ٳ��Ĵ�ֱ�߶�FH��30�ף�����ѧ¥����ϯ̨�ľ���AC��60�ף�б��CD���½���45�㣬б��EF���¶�i=3��4����·��DE��CHƽ�У���DE���ӳ�����FH�Ľ���K����FH�е㣬CH�ij���40�ף�FG�ij���50�ף�һ��ѧ��������ѧ¥����������¥����ѧ��¼������A-C-D-E-F-G·�ߣ��������ٶȶ�Ϊ40��/���ӣ�ƽ���ٶȶ�Ϊ50��/���ӣ��ʸ�ѧ����������¥��ʱ���Ƕ��٣���$\sqrt{2}$��1.4��
��ͼ��У������ʯ���ٳ��Ĵ�ֱ�߶�FH��30�ף�����ѧ¥����ϯ̨�ľ���AC��60�ף�б��CD���½���45�㣬б��EF���¶�i=3��4����·��DE��CHƽ�У���DE���ӳ�����FH�Ľ���K����FH�е㣬CH�ij���40�ף�FG�ij���50�ף�һ��ѧ��������ѧ¥����������¥����ѧ��¼������A-C-D-E-F-G·�ߣ��������ٶȶ�Ϊ40��/���ӣ�ƽ���ٶȶ�Ϊ50��/���ӣ��ʸ�ѧ����������¥��ʱ���Ƕ��٣���$\sqrt{2}$��1.4�� ���� ��������ֱ�ó�DE��DN��EF�ij�������������·�̳����ٶȵó����ɣ�
��� 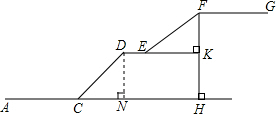 �⣺����D��DN��CH�ڵ�N��
�⣺����D��DN��CH�ڵ�N��
��FH=30m��KΪFH���е㣬
��FK=KH=15m��
��DN=15m��
��б��CD���½���45�㣬б��EF���¶�i=3��4��
��CN=15m����CD=15$\sqrt{2}$m��FK��EK=3��4��
��EK=20m����EF=25m��
��DE=CH-CN-EK=40-15-20=5��m����
�ʸ�ѧ����������¥��ʱ���ǣ�$\frac{FE+CD}{40}$+$\frac{AC+DE+FG}{50}$=$\frac{15\sqrt{2}+25}{40}$+$\frac{60+5+50}{50}$=3.45�����ӣ���
�𣺸�ѧ����������¥��ʱ����3.45�֣�
���� ������Ҫ�����˽�ֱ�������ε�Ӧ�ã���������ó�DE�ij��ǽ���ؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -8 | B�� | 2 | C�� | 2��-2 | D�� | 8��-8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 32 | C�� | -$\frac{25}{7}$ | D�� | $\frac{25}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a=3��b=4��c=5 | B�� | a=12��b=13��c=5 | C�� | a=15��b=8��c=17 | D�� | a=13��b=14��c=15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?BFDE�У��ֱ��ӳ�DF��C��BE��A��ʹ��DF=FC��BE=EA����֤���ı���ABCD��ƽ���ı��Σ�
��ͼ����?BFDE�У��ֱ��ӳ�DF��C��BE��A��ʹ��DF=FC��BE=EA����֤���ı���ABCD��ƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com