
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF. 
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
【答案】
(1)解:平行;
证明:∵∠2+∠CDB=180°,∠1+∠2=180°,
∴∠CDB=∠1,
∴AE∥FC
(2)解:平行,
证明:∵AE∥FC,
∴∠CDA+∠DAE=180°,
∵∠DAE=∠BCF
∴∠CDA+∠BCF=180°,
∴AD∥BC
(3)解:平分,
证明:∵AE∥FC,
∴∠EBC=∠BCF,
∵AD∥BC,
∴∠BCF=∠FDA,∠DBC=∠BDA,
又∵DA平分∠BDF,即∠FDA=∠BDA,
∴∠EBC=∠DBC,
∴BC平分∠DBE.
【解析】(1)∠1+∠2=180°而∠2+∠CDB=180°,则∠CDB=∠1,根据同位角相等,两直线平行,求得结论;(2)要说明AD与BC平行,只要说明∠BCF+∠CDA=180°即可.而根据AE∥FC可得:∠CDA+∠DEA=180°,再据∠DAE=∠BCF就可以证得.(3)BC平分∠DBE即说明∠EBC=∠DBC是否成立.根据AE∥FC,可得:∠EBC=∠BCF,据AD∥BC得到:∠BCF=∠FAD,∠DBC=∠BAD,进而就可以证出结论.
【考点精析】根据题目的已知条件,利用平行线的判定的相关知识可以得到问题的答案,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.


科目:初中数学 来源: 题型:
【题目】我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
【1】请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
【2】如图,在![]() 中,点
中,点![]() 分别在
分别在![]() 上,设
上,设![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() .请你写出图中一个与
.请你写出图中一个与![]() 相等的角,并猜想图中哪个四边形是等对边四边形;
相等的角,并猜想图中哪个四边形是等对边四边形;

【3】在![]() 中,如果
中,如果![]() 是不等于
是不等于![]() 的锐角,点
的锐角,点![]() 分别在
分别在![]() 上,且
上,且![]() .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了求1+2+22+23+24+…+22018的值,可以设s=1+2+22+23+…+22018 , 则则2s=2+22+23+24+…+22018 , 所以2s﹣s=22019﹣1,即1+2+22+…+22018=22019﹣1,仿照以上推理,计算出1+7+72+73+…72020的值( )
A.72021﹣1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝间距离的最大值为( )

A.5 B.6 C.7 D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月完工的上海中心大厦是一座超高层地标式摩天大楼,其高度仅次于世界排名第一的阿联酋迪拜大厦,某人从距离地面高度263米的东方明珠球体观光层测得上海中心大厦顶部的仰角是22.3°.已知东方明珠与上海中心大厦的水平距离约为900米,那么上海中心大厦的高度约为 米(精确到1米).(参考数据:sin22.3°≈0.38,cos22.3°≈0.93.tan22.3°≈0.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
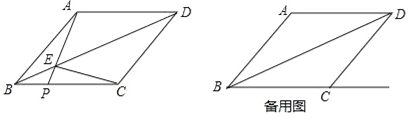
【题目】已知:如图,在菱形ABCD中,AB=5,联结BD,sin∠ABD=![]() .点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
.点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
(1)求证:AE=CE;
(2)当点P在线段BC上时,设BP=x,△PEC的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)当点P在线段BC的延长线上时,若△PEC是直角三角形,求线段BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com