
【题目】如图1,在正方形ABCD中,O是对角线AC上一点,点E在BC的延长线上,且OE = OB.
(1)求证:△OBC ≌ △ODC.
(2)求证:∠DOE = ∠ABC.
(3)把正方形ABCD改为菱形,其他条件不变(如图2),若∠ABC = 52° ,求∠DOE的度数.
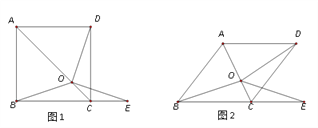
【答案】(1)证明见解析; (2)证明见解析; (3)52°.
【解析】试题分析:(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCO=∠DCO,然后利用“边角边”证明即可;
(2)根据全等三角形对应角相等可得∠CBO=∠CDO,根据等边对等角可得∠CBO=∠E,然后求出∠DOE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得证;
(3)根据(2)的结论解答.
试题解析(1)证明:在正方形ABCD中,BC=DC,∠BCO=∠DCO=45°,
∵在△BCO和△DCO中,
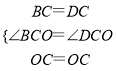 ,
,
∴△BCO≌△DCO(SAS);
(2)由(1)知,△BCO≌△DCO,
∴∠CBO=∠CDO,
∵OE=OB,
∴∠CBO=∠E,
∵∠1=∠2(对顶角相等),
∴180°-∠1-∠CDO=180°-∠2-∠E,
即∠DOE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DOE=∠ABC;
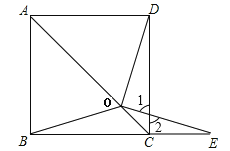
(3)解:与(2)同理可得:∠DOE=∠ABC,
∵∠ABC=52°,
∴∠DPE=52°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,已知AB>BC.
(1)实践与操作:作∠ADC的平分线交AB于点E,在DC上截取DF=AD,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形AEFD的形状,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
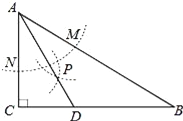
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人设计了一个游戏,在网吧征求了三位游戏迷的意见,就宣传“本游戏深受大家欢迎”,这种做法是错误的,原因是( )
A. 没有经过专家鉴定
B. 应调查4位游戏迷
C. 调查数量太少,且不具有代表性
D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂共有120名生产工人,每个工人每天可生产螺栓25个或螺母20个,如果一个螺栓与两个螺母配成一套 ,那么每天安排多名工人生产螺栓,多少名工人生产螺母,才能使每天生产出来的产品配成最多套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com