
”¾ĢāÄæ”æČēĶ¼£¬°ė¾¶ĪŖ 1 µÄŠ”Ō²Óė°ė¾¶ĪŖ 2 µÄ“óŌ²£¬ÓŠŅ»øö¹«¹²µćÓėŹżÖįÉĻµÄŌµćÖŲŗĻ£¬Į½Ō²ŌŚŹżÖįÉĻ×öĪŽ»¬¶ÆµÄ¹ö¶Æ£¬Š”Ō²µÄŌĖ¶ÆĖŁ¶ČĪŖĆæĆė¦Šøöµ„Ī»£¬“óŌ²µÄŌĖ¶ÆĖŁ¶ČĪŖĆæĆė 2¦Šøöµ„Ī»£¬
£Ø1£©ČōŠ”Ō²²»¶Æ£¬“óŌ²ŃŲŹżÖįĄ“»Ų¹ö¶Æ£¬¹ę¶Ø“óŌ²ĻņÓŅ¹ö¶ÆµÄŹ±¼ä¼ĒĪŖÕżŹż£¬Ļņ×ó¹ö¶ÆŹ±¼ä¼“ĪŖøŗŹż£¬ŅĄ“Ī¹ö¶ÆµÄĒéæöĀ¼ČēĻĀ£Øµ„Ī»£ŗĆė£©£ŗ
©1£¬+2£¬©4£¬©2£¬+3£¬+6
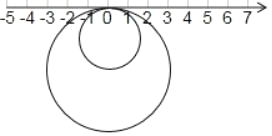
¢ŁµŚ “Ī¹ö¶Æŗ󣬓óŌ²ÓėŹżÖįµÄ¹«¹²µćµ½ŌµćµÄ¾ąĄė×īŌ¶£»
¢Śµ±“óŌ²½įŹųŌĖ¶ÆŹ±£¬“óŌ²ŌĖ¶ÆµÄĀ·³Ģ¹²ÓŠ¶ąÉŁ£æ“ĖŹ±Į½Ō²ÓėŹżÖįÖŲŗĻµÄµćÖ®¼äµÄ¾ąĄėŹĒ¶ąÉŁ£æ£Ø½į¹ū±£Įō¦Š£©
£Ø2£©ČōĮ½Ō²Ķ¬Ź±ŌŚŹżÖįÉĻø÷×ŌŃŲ×ÅijŅ»·½ĻņĮ¬Šų¹ö¶Æ£¬¹ö¶ÆŅ»¶ĪŹ±¼äŗóĮ½Ō²ÓėŹżÖįÖŲŗĻµÄµćÖ®¼äĻą¾ą 9¦Š£¬Ēó“ĖŹ±Į½Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹż£®
”¾“š°ø”æ(1)¢Ł4¢Ś8¦Š;(2)Š”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©3¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ6¦Š.
»ņŠ”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ3¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©6¦Š
”¾½āĪö”æ
£Ø1£©¢ŁĖć³öĆæ“Ī¹ö¶Æŗó“óŌ²ÓėŹżÖįµÄ¹«¹²µćµ½ŌµćµÄ¾ąĄė£¬Č»ŗó±Č½Ļ“󊔼“æÉ£»¢Ś×ÜĀ·³ĢÓė·½ĻņĪŽ¹Ų°ŃĆæ“ĪµÄŅĘ¶ÆµÄ¾ąĄėĻą¼Ó¼“æÉ£»
£Ø2£©·ÖĶ¬ĻņŗĶ·“ĻąĮ½ÖÖĒéæöĢÖĀŪ£¬Ķ¬ĻņĀ·³ĢÖ®²īĪŖ9¦Š£¬·“ĻņĀ·³ĢÖ®ŗĶĪŖ9¦Š£¬Č»ŗóĒó³öĻąÓ¦Ź±¼ä£¬ŌŁøł¾Ż²»Ķ¬·½ĻņČ·¶ØĮ½Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹż.
½ā£ŗ£Ø1£©¢Ł£ŗµŚ1“Ī¹ö¶Æŗ󣬓óŌ²ÓėŹżÖįµÄ¹«¹²µćµ½ŌµćµÄ¾ąĄė£ŗ|©1”Į2¦Š|£½2¦Š
µŚ2“Ī¹ö¶Æŗ󣬓óŌ²ÓėŹżÖįµÄ¹«¹²µćµ½ŌµćµÄ¾ąĄė£ŗ|©1”Į2¦Š+2”Į2¦Š|£½2¦Š
µŚ3“Ī¹ö¶Æŗ󣬓óŌ²ÓėŹżÖįµÄ¹«¹²µćµ½ŌµćµÄ¾ąĄė£ŗ|©1”Į2¦Š+2”Į2¦Š©4”Į2¦Š|£½6¦Š
µŚ4“Ī¹ö¶Æŗ󣬓óŌ²ÓėŹżÖįµÄ¹«¹²µćµ½ŌµćµÄ¾ąĄė£ŗ|©1”Į2¦Š+2”Į2¦Š©4”Į2¦Š©2”Į2¦Š|£½10¦Š
µŚ5“Ī¹ö¶Æŗ󣬓óŌ²ÓėŹżÖįµÄ¹«¹²µćµ½ŌµćµÄ¾ąĄė£ŗ|©1”Į2¦Š+2”Į2¦Š©4”Į2¦Š©2”Į2¦Š+3”Į2¦Š|£½4¦Š
µŚ6“Ī¹ö¶Æŗ󣬓óŌ²ÓėŹżÖįµÄ¹«¹²µćµ½ŌµćµÄ¾ąĄė£ŗ|©1”Į2¦Š+2”Į2¦Š©4”Į2¦Š©2”Į2¦Š+3”Į2¦Š+6”Į2¦Š|£½8¦Š£¬ĖłŅŌµŚĖÄ“Ī¹ö¶Æŗó“óŌ²ÓėŹżÖįµÄ¹«¹²µćµ½ŌµćµÄ¾ąĄė×īŌ¶£®¹Ź“š°øĪŖ4£»
¢Ś×ÜĀ·³ĢĪŖ£ŗ|©1”Į2¦Š|+|+2”Į2¦Š|+|©4”Į2¦Š|+|©2”Į2¦Š|+|+3”Į2¦Š|+|+6”Į2¦Š|£½36¦Š
“ĖŹ±Į½Ō²ÓėŹżÖįÖŲŗĻµÄµćÖ®¼äµÄ¾ąĄėĪŖ£ŗ|©1”Į2¦Š+2”Į2¦Š©4”Į2¦Š©2”Į2¦Š+3”Į2¦Š+6”Į2¦Š|£½8¦Š
£Ø2£©µ±ĖüĆĒĶ¬ĻņŌĖ¶ÆŹ±![]() Ćė£¬Š”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ9¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ18¦Š£¬»ņŠ”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©9¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©18¦Š£¬µ±ĖüĆĒ·“ĻņŌĖ¶ÆŹ±
Ćė£¬Š”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ9¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ18¦Š£¬»ņŠ”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©9¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©18¦Š£¬µ±ĖüĆĒ·“ĻņŌĖ¶ÆŹ±![]() Ćė£¬Š”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©3¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ6¦Š£¬»ņŠ”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ3¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©6¦Š.
Ćė£¬Š”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©3¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ6¦Š£¬»ņŠ”Ō²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ3¦Š£¬“óŌ²ÓėŹżÖįÖŲŗĻµÄµćĖł±ķŹ¾µÄŹżĪŖ©6¦Š.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĒų¶Ō¼“½«²Ī¼ÓÖŠæ¼µÄ4 000Ćū³õÖŠ±ĻŅµÉś½ųŠŠĮĖŅ»“ĪŹÓĮ¦³éŃłµ÷²é£¬»ęÖĘ³öʵŹż·Ö²¼±ķŗĶ²»ĶźÕūµÄʵŹż·Ö²¼Ö±·½Ķ¼£®Ēėøł¾ŻĶ¼±ķŠÅĻ¢»Ų“šĻĀĮŠĪŹĢā£ŗ
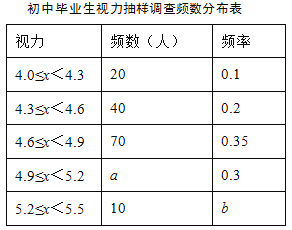
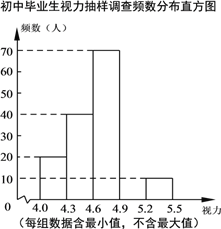
£Ø1£©±¾“Īµ÷²éŃł±¾ČŻĮæĪŖ”” £»
£Ø2£©ŌŚĘµŹż·Ö²¼±ķÖŠ£¬a£½”” ””£¬b£½”” ””£¬²¢½«ĘµŹż·Ö²¼Ö±·½Ķ¼²¹³äĶźÕū£»
£Ø3£©ČōŹÓĮ¦ŌŚ4.9ŅŌÉĻ£Øŗ¬4.9£©¾łŹō±ź×¼ŹÓĮ¦£¬øł¾ŻÉĻŹöŠÅĻ¢¹Ą¼ĘČ«Ēų³õÖŠ±ĻŅµÉśÖŠ“ļµ½±ź×¼ŹÓĮ¦µÄѧɜŌ¼ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ČĖŌŚ±ŹÖ±µÄŗž±ß¹«Ā·ÉĻĶ¬Ęšµć”¢Ķ¬ÖÕµć”¢Ķ¬·½ĻņŌČĖŁ²½ŠŠ2400Ć×£¬Ļȵ½ÖÕµćµÄČĖŌµŲŠŻĻ¢£®ŅŃÖŖ¼×ĻČ³ö·¢4·ÖÖÓ£¬ŌŚÕūøö²½ŠŠ¹ż³ĢÖŠ£¬¼×”¢ŅŅĮ½ČĖµÄ¾ąĄėy£ØĆ×£©Óė¼×³ö·¢µÄŹ±¼ät£Ø·Ö£©Ö®¼äµÄ¹ŲĻµČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪ£ŗ
¢Ł¼×²½ŠŠµÄĖŁ¶ČĪŖ60Ć×/·Ö£»
¢ŚŅŅ×ßĶźČ«³ĢÓĆĮĖ32·ÖÖÓ£»
¢ŪŅŅÓĆ16·ÖÖÓ×·ÉĻ¼×£»
¢ÜŅŅµ½“ļÖÕµćŹ±£¬¼×ĄėÖÕµć»¹ÓŠ300Ć×
ĘäÖŠÕżČ·µÄ½įĀŪÓŠ£Ø””””£©
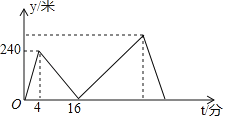
A. 1øö B. 2øö C. 3øö D. 4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»Į¾Ęū³µŌŚÄ³“ĪŠŠŹ»¹ż³ĢÖŠ£¬ÓĶĻäÖŠµÄŹ£ÓąÓĶĮæy£ØÉż£©ÓėŠŠŹ»Ā·³Ģx£ØĒ§Ć×£©Ö®¼äŹĒŅ»“ĪŗÆŹż¹ŲĻµ£¬Ęä²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£®
£Ø1£©Ēóy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£»£Ø²»ŠčŅŖŠ“¶ØŅåÓņ£©
£Ø2£©ŅŃÖŖµ±ÓĶĻäÖŠµÄŹ£ÓąÓĶĮæĪŖ8ÉżŹ±£¬øĆĘū³µ»įæŖŹ¼ĢįŹ¾¼ÓÓĶ£¬ŌŚ“Ė“ĪŠŠŹ»¹ż³ĢÖŠ£¬ŠŠŹ»ĮĖ500Ē§Ć׏±£¬Ė¾»ś·¢ĻÖĄėĒ°·½×ī½üµÄ¼ÓÓĶÕ¾ÓŠ30Ē§Ć×µÄĀ·³Ģ£¬ŌŚæŖĶłøĆ¼ÓÓĶÕ¾µÄĶ¾ÖŠ£¬Ęū³µæŖŹ¼ĢįŹ¾¼ÓÓĶ£¬ÕāŹ±Ąė¼ÓÓĶÕ¾µÄĀ·³ĢŹĒ¶ąÉŁĒ§Ć×£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹŠĪŖĮĖ½ā¾ÅÄź¼¶Ń§ÉśµÄÉķĢåĖŲÖŹ²āŹŌĒéæö£¬Ė껜³éČ”ĮĖøĆŹŠ¾ÅÄź¼¶²æ·ÖѧɜµÄÉķĢåĖŲÖŹ²āŹŌ³É¼Ø×÷ĪŖŃł±¾£¬°“A£ØÓÅŠć£©£¬B£ØĮ¼ŗĆ£©£¬C£ØŗĻøń£©£¬D£Ø²»ŗĻøń£©ĖÄøöµČ¼¶½ųŠŠĶ³¼Ę£¬²¢½«Ķ³¼Ę½į¹ū»ęÖĘĮĖĻĀĆęĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬Ēėøł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ

£Ø1£©“Ė“Ī¹²µ÷²éĮĖ¶ąÉŁĆūѧɜ£æ
£Ø2£©½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£¬²¢¼ĘĖćÉČŠĪĶ³¼ĘĶ¼ÖŠ”°A”±²æ·ÖĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹż£®
£Ø3£©øĆŹŠ¾ÅÄź¼¶¹²ÓŠ8000Ćūѧɜ²Ī¼ÓĮĖÉķĢåĖŲÖŹ²āŹŌ£¬¹Ą¼Ę²āŹŌ³É¼ØŌŚĮ¼ŗĆŅŌÉĻ£Øŗ¬Į¼ŗĆ£©µÄČĖŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¶ž“ĪŗÆŹżĶ¼ĻóµÄ¶Ō³ĘÖįĪŖÖ±Ļßx=2£¬¶„µćĪŖµćC£¬Ö±Ļßy=x+mÓėøƶž“ĪŗÆŹżµÄĶ¼Ļó½»ÓŚµćA£¬BĮ½µć£¬ĘäÖŠµćAµÄ×ų±źĪŖ£Ø5£¬8£©£¬µćBŌŚyÖįÉĻ£®
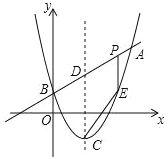
£Ø1£©ĒómµÄÖµŗĶøƶž“ĪŗÆŹżµÄ±ķ“ļŹ½£®ĪŖĻ߶ĪABÉĻŅ»øö¶Æµć£ØµćP²»ÓėA£¬BĮ½µćÖŲŗĻ£©£¬¹żµćP×÷xÖįµÄ“¹Ļߣ¬ÓėÕāøö¶ž“ĪŗÆŹżµÄĶ¼Ļó½»ÓŚµćE£®
¢ŁÉčĻ߶ĪPEµÄ³¤ĪŖh£¬ĒóhÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮæxµÄȔֵ·¶Ī§£®
¢ŚČōÖ±ĻßABÓėÕāøö¶ž“ĪŗÆŹżĶ¼ĻóµÄ¶Ō³ĘÖįµÄ½»µćĪŖD£¬Ēóµ±ĖıߊĪDCEPŹĒĘ½ŠŠĖıߊĪŹ±µćPµÄ×ų±ź£®
£Ø3£©ČōµćP£Øx£¬y£©ĪŖÖ±ĻßABÉĻµÄŅ»øö¶Æµć£¬ŹŌĢ½¾æ£ŗŅŌPBĪŖÖ±¾¶µÄŌ²ÄÜ·ńÓė×ų±źÖįĻąĒŠ£æČē¹ūÄÜĒėĒó³öµćPµÄ×ų±ź£¬Čē¹ū²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŹżÖįÉĻµćA£¬B·Ö±š¶ŌÓ¦Źża£¬b£¬ĘäÖŠa£¼0£¬b£¾0£®
£Ø1£©µ±a£½©2£¬b£½6Ź±£¬Ļ߶ĪABµÄÖŠµć¶ŌÓ¦µÄŹżŹĒ”” ””£»£ØÖ±½ÓĢī½į¹ū£©
£Ø2£©ČōøĆŹżÖįÉĻĮķÓŠŅ»µćM¶ŌÓ¦×ÅŹżm£®
¢Łµ±m£½2£¬b£¾2£¬ĒŅAM£½2BMŹ±£¬Ē󓜏żŹ½a+2b+20µÄÖµ£»
¢Śµ±a£½©2£¬ĒŅAM£½3BMŹ±£¬ĒėĖµĆ÷“śŹżŹ½3b©4m»ņ2m©3b¾łÓŠ¶ØÖµ£Ø²»±äµÄŹżÖµ£©£¬²¢Ēó³öĖüĆĒµÄ¶ØÖµ£®
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹży=kx+bµÄĶ¼Ļó¾¹żA£Ø©2£¬©1£©£¬B£Ø1£¬3£©Į½µć£¬²¢ĒŅ½»xÖįÓŚµćC£¬½»yÖįÓŚµćD£®
£Ø1£©ĒóøĆŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©Ēó”÷AOBµÄĆ껿£®
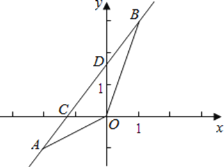
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼AŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹżĪŖ-2.
(1)µćBŌŚµćAÓŅ±ß¾ąĄėAµć4øöµ„Ī»³¤¶Č£¬ŌņµćBĖł¶ŌÓ¦µÄŹżŹĒ_____.
(2)ŌŚ(1)µÄĢõ¼žĻĀ£¬µćAŅŌĆæĆė2øöµ„Ī»³¤¶ČŃŲŹżÖįĻņ×óŌĖ¶Æ£¬µćBŅŌĆæĆė3øöµ„Ī»³¤¶ČŃŲŹżÖįĻņÓŅŌĖ¶Æ.ĻÖĮ½µćĶ¬Ź±ŌĖ¶Æ,µ±µćAŌĖ¶Æµ½-6µÄµć“¦Ź±£¬ĒóA”¢BĮ½µć¼äµÄ¾ąĄė.
(3)ŌŚ(2)µÄĢõ¼žĻĀ£¬ĻÖAµć¾²Ö¹²»¶Æ£¬BµćŅŌŌĖŁŃŲŹżÖįĻņ×óŌĖ¶Æ£¬¾¹ż¶ą³¤Ź±¼äA”¢BĮ½µćĻą¾ą4øöµ„Ī»³¤¶Č.
![]()
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com