
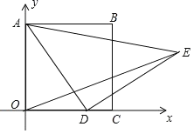
【题目】如图,在平面直角坐标系中,已知正方形 ABCO,边长是 4,点 D(a,0),以 AD 为边在AD 的右侧作等腰 Rt△ADE,∠ADE=90°,连接 OE,则 OE 的最小值为__________________.
【答案】![]()
【解析】
如图,作EH⊥x轴于H,连接CE.利用全等三角形的性质证明∠ECH=45°,推出点E在直线y=x4上运动,作OE′⊥CE,求出OE′的长即可解决问题;
如图,作EH⊥x轴于H,连接CE.
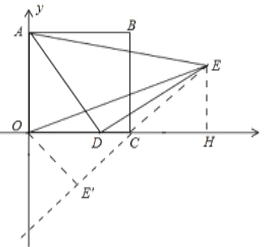
∵∠AOD=∠ADE=∠EHD=90°,
∴∠ADO+∠EDH=90°,∠EDH+∠DEH=90°,
∴∠ADO=∠DEH,
∵AD=DE,
∴△ADO≌△DEH(AAS),
∴OA=DH=OC=4,OD=EH,
∴OD=CH=EH,
∴∠ECH=45°,
故可设CE直线的解析式为y=x+b
把C(4,0)代入得0=4+b
解得b=-4
∴CE直线的解析式为y=x-4
∴点E在直线y=x4上运动,作OE′⊥CE,则△OCE′是等腰直角三角形,
∴CE’=OE’
∵OC=4,
∴CE’2+OE’2=OC2,
即2OE’2=42,
解得OE′=![]() ,
,
∴OE的最小值为![]() .
.
故答案为:![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两种商品,已知买一件
两种商品,已知买一件![]() 商品要比买一件
商品要比买一件![]() 商品少
商品少![]() 元,用
元,用![]() 元全部购买
元全部购买![]() 商品的数量与用
商品的数量与用![]() 元全部购买
元全部购买![]() 商品的数量相同.
商品的数量相同.
(1)求![]() 、
、![]() 两种商品每件各是多少元?
两种商品每件各是多少元?
(2)如果小亮准备购买![]() 、
、![]() 两种商品共
两种商品共![]() 件,总费用不超过
件,总费用不超过![]() 元,且不低于
元,且不低于![]() 元,问有几种购买方案,哪种方案费用最低?
元,问有几种购买方案,哪种方案费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是
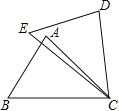
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系xOy中,若A(0,4)、B(1,0)且以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
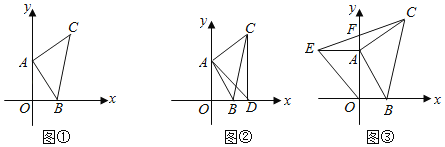
(1)如图1,求C点坐标;
(2)如图2,在图1中过C点作CD⊥x轴于D,连接AD,求∠ADC的度数;
(3)如图3,点A在y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
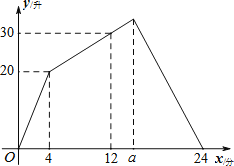
【题目】一个有进水管与出水管的容器,从某时刻开始的4分内只进水不出水,在随后的若干分内既进水又出水,之后只有出水不进水,每分钟的进水量和出水量是两个常数,容器内的水量![]() (单位:升)与时间
(单位:升)与时间![]() (单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,
(单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育场上,老师用绳子围成一个周长为![]() 的游戏场地,围成的场地是如图所示的矩形
的游戏场地,围成的场地是如图所示的矩形![]() ,设
,设![]() 的长为
的长为![]() (
(![]() 取整数),矩形
取整数),矩形![]() 的面积为
的面积为![]() .
.
⑴.写出![]() 与
与![]() 之间的函数关系式,求出
之间的函数关系式,求出![]() 的最值和相应的
的最值和相应的![]() 的值;
的值;
⑵.若矩形![]() 的面积为
的面积为![]() 且
且![]() ,请求出此时
,请求出此时![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表:

那么关于它的图象,下列判断正确的是( )
A. 开口向上 B. 与x轴的另一个交点是(3,0)
C. 与y轴交于负半轴 D. 在直线x=1的左侧部分是下降的
查看答案和解析>>
科目:初中数学 来源: 题型:
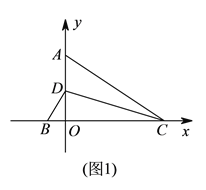
【题目】如图![]() ,点
,点![]() 、
、![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 、
、![]() 分别在
分别在![]() 轴上,
轴上, ![]() 平分
平分![]() ,与
,与![]() 轴交于
轴交于![]() 点,
点, ![]() .
.
(![]() )求证:
)求证: ![]() .
.
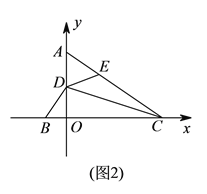
(![]() )如图
)如图![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为
为![]() 上一点,且
上一点,且![]() ,求
,求![]() 的长.
的长.
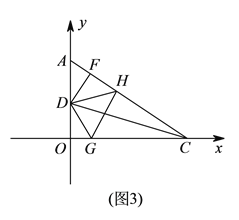
(![]() )如图
)如图![]() ,过
,过![]() 作
作![]() 于
于![]() 点,点
点,点![]() 为
为![]() 上一动点,点
上一动点,点![]() 为
为![]() 上一动点,当
上一动点,当![]() 在
在![]() 上移动、点
上移动、点![]() 在
在![]() 上移动时,始终满足
上移动时,始终满足![]() ,试判断
,试判断![]() 、
、![]() 、
、![]() 这三者之间的数量关系,写出你的结论并加以证明.
这三者之间的数量关系,写出你的结论并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com