
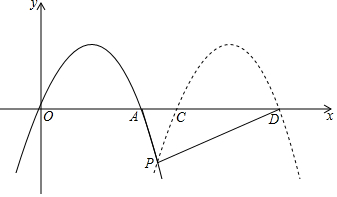
 如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )
如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )| A. | $\frac{m}{2}$(m2-4) | B. | $\frac{1}{2}$m2-2 | C. | $\frac{m}{2}$(4-m2) | D. | 2-$\frac{1}{2}$m2 |
分析 先求出A的坐标,设P关于x=1的对称点为Q,且设P的横坐标为x1,Q的横坐标为x2,根据题意可知x1+x2=2,x1-x2=m,从而求出x1与x2的表达式,
解答  解:抛物线的对称轴为:x=1,
解:抛物线的对称轴为:x=1,
令y=0代入y=-2x2+4x,
∴0=-2x2+4x,
∴x=0或x=2,
∴A(2,0)
∴OA=2,
设P关于x=1的对称点为Q,且设P的横坐标为x1,Q的横坐标为x2,
∴$\frac{{x}_{1}+{x}_{2}}{2}=1$,
∵抛物线向右平移m(m>2)个单位长度,
∴PQ=m,
∴x1-x2=m,
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2}\\{{x}_{1}-{x}_{2}=m}\end{array}\right.$
解得:x1=$\frac{m+2}{2}$,x2=$\frac{2-m}{2}$
把x1=$\frac{m+2}{2}$代入y=-2x2+4x
∴y=2-$\frac{{m}^{2}}{2}$<0
∴在△PCD中,CD边上的高为:$\frac{{m}^{2}}{2}$-2,
∵OA=CD=2,
∴S△PCD=$\frac{1}{2}$×2×($\frac{{m}^{2}}{2}-2$)=$\frac{{m}^{2}}{2}$-2
故选(B)
点评 本题考查抛物线与x轴的交点,解题的关键是求出P的坐标,然后根据三角形面积公式即可求出△PCD的面积,本题属于中等题型.


科目:初中数学 来源: 题型:选择题
| x | 6.17 | 6.18 | 6.19 |
| y | -0.03 | -0.01 | 0.02 |
| A. | -0.03<x<-0.01 | B. | -0.01<x<0.02 | C. | 6.18<x<6.19 | D. | 6.17<x<6.18 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
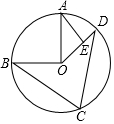 如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )
如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
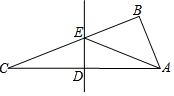 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com