
【题目】如图,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与顶点A,B,D重合,∠AEF=∠BCE,圈O过A,E,F三点. 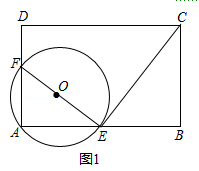
(1)求证:圈O与CE相切与点E;
(2)如图1,若AF=2FD且∠AEF=30°,求n的值; 
(3)如图2.若EF=EC且圈O与边CD相切,求n的值. 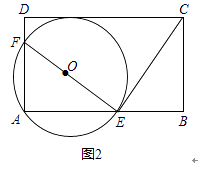
【答案】
(1)证明:在矩形ABCD中,∠A=∠B=90°,
∴圆心O是EF的中点;
∵∠AEF=∠BCE,∠BEC+∠BCE=90°,
∴∠BEC+∠AEF=90°,
即∠FEC=90°,
∴圆O与CE相切与点E
(2)解:如图1,设FD=x,AF=2x;
则BC=3x;
∵∠AEF=30°,
∴AE=AFtan 30°=2 ![]() x,
x,
∵∠BCE=30°,
∴BE=BCtan30°= ![]() x,
x,
∴AB=3 ![]() x,
x,
∴n= ![]() =
= ![]()
(3)解:设切点为G,连OG并延长交AE于点H;
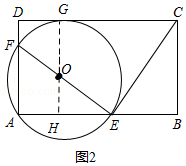
在△AEF与△BCE中,
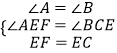
∴△AEF≌△BCE(AAS)
设BC=AE=y,
则BE=AF=(n﹣1)y,
HE= ![]() AE=
AE= ![]() y
y
∴由切线的性质可知:OG=OE=OF,
∴由中位线的性质可知:OH= ![]() AF=
AF= ![]()
∴OE=OG=y﹣ ![]() y=
y= ![]() y,
y,
∴Rt△OHE中,由勾股定理可知:
( ![]() )2=(
)2=( ![]() )2+(
)2+( ![]() )2,
)2,
解得:n= ![]()
【解析】(1)只需要证明∠FEC=90°即可,由于∠AEF=∠BCE,∠BEC+∠BCE=90°,所以∠BEC+∠AEF=90°,(2)设FD=x,AF=2x,所以BC=3x,根据特殊角的锐角三角函数值即可求出BE、AB的长度,从而可求出n的值.(3)设切点为G,连OG并延长交AE于点H;,先证明△AEF≌△BCE,然后根据AB=nAD,可设BC=y,然后用y表示OH、OE,HE的长度,根据勾股定理即可求出n的值.


科目:初中数学 来源: 题型:
【题目】计算
(1)(![]() )×(﹣36)
)×(﹣36)
(2)﹣32+(﹣![]() )2×(﹣
)2×(﹣![]() )+|﹣22|+(﹣1)2013;
)+|﹣22|+(﹣1)2013;
(3)36×(﹣99![]() );
);
(4)﹣13×![]() ﹣0.34×
﹣0.34×![]() +
+![]() ×(﹣13)﹣
×(﹣13)﹣![]() ×0.34(用简便方法计算)
×0.34(用简便方法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
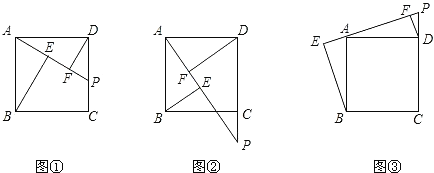
【题目】在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B、D作![]() 、
、![]() ,垂足分别为E、F.
,垂足分别为E、F.
![]() 如图
如图![]() ,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?
,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?
![]() 若点P在DC的延长线上,如图
若点P在DC的延长线上,如图![]() ,那么这三条线段的长度之间又具有怎样的数量关系?
,那么这三条线段的长度之间又具有怎样的数量关系?
![]() 若点P在CD的延长线上,如图
若点P在CD的延长线上,如图![]() ,请直接写出结论.
,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】之前我们学习了一元一次方程的解法,下面是一道解一元一次方程的题:
解方程![]() ﹣
﹣![]() =1
=1
老师说:这是一道含有分母的一元一次方程,我们可以根据等式的性质,可以把方程的两边同乘以6,这样就可以去掉分母了.于是,小明按照老师说的方法进行了解答,小明同学的解题过程如下:
解:方程两边同时乘以6,得![]() ×6﹣
×6﹣![]() ×6=1…………①
×6=1…………①
去分母,得:2(2﹣3x)﹣3(x﹣5)=1………②
去括号,得:4﹣6x﹣3x+15=1……………③
移项,得:﹣6x﹣3x=1﹣4﹣15…………④
合并同类项,得﹣9x=﹣18……………⑤
系数化1,得:x=2………………⑥
上述小明的解题过程从第 步开始出现错误,错误的原因是 .
请帮小明改正错误,写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,将菱形沿EF折叠,点B正好落在AD边的点G处,且EG⊥AC,若CD=8,则FG的长为( ) 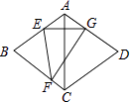
A.4 ![]()
B.4 ![]()
C.4 ![]()
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB⊥BC且AB=BC,CD⊥DE且CD=DE,请按照图中所标注的数据,计算图中实线所围成的图形面积是( )
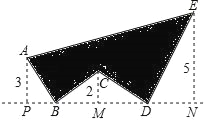
A. 64 B. 50 C. 48 D. 32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com