设关于x的二次方程(a2+1)x2-4ax+2=0的两根为x1,x2,若2x1x2=x1-3x2,试求a的值.
【答案】
分析:先根据一元二次方程根与系数的关系得出x
1+x
2及x
1•x
2,代入2x
1x
2=x
1-3x
2中即可求出a的值,再把所得a的值代入原方程检验即可.
解答:解:∵关于x的二次方程(a
2+1)x
2-4ax+2=0的两根为x
1,x
2,
∴
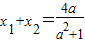
①,
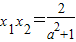
②
∵2x
1x
2=x
1-3x
2,
∴2x
1x
2+(x
1+x
2)=2(x
1-x
2),平方得4(x
1x
2)
2+4x
1x
2(x
1+x
2)=3(x
1+x
2)
2-16x
1x
2,
将式①、②代入后,解得a=3,a=-1,
当a=3时,原方程可化为10x
2-12x+2=0,△=12
2-4×10×2=64>0,原方程成立;
当a=-1时,原方程可化为2x
2+4x+2=0,△=4
2-4×2×2=0,原方程成立.
∴a=3或a=-1.
点评:本题考查的是一元二次方程根与系数的关系,在解答此类题目时一定要把所得结果代入原方程进行检验,舍去不合题意的未知数的值.

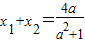 ①,
①,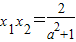 ②
②
