
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| A、(1,3) |
| B、(1,-3) |
| C、(-1,3) |
| D、(-1,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:
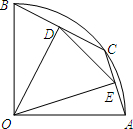 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E,则线段DE的长为( )
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E,则线段DE的长为( )A、2
| ||
B、
| ||
C、
| ||
| D、1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
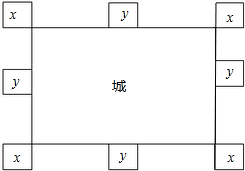 戚继光是古代著名的抗倭将领,有一次,当倭寇来袭时,戚家军主力尚未到达,城里的兵力仅360人,戚继光思考着怎样布置兵力,使敌人不论从哪一方向察看,都有100名士兵在把手,经过思考,戚继光决定抽调100人去绕道袭击敌人的粮草.有人担心城内兵力太少,戚继光却说:“没关系,我会重新布置,这260人在布置好后,敌人无论从哪一面察看,反而会认为士兵增加了25名.”随后他画了一张图让大家看(如图)
戚继光是古代著名的抗倭将领,有一次,当倭寇来袭时,戚家军主力尚未到达,城里的兵力仅360人,戚继光思考着怎样布置兵力,使敌人不论从哪一方向察看,都有100名士兵在把手,经过思考,戚继光决定抽调100人去绕道袭击敌人的粮草.有人担心城内兵力太少,戚继光却说:“没关系,我会重新布置,这260人在布置好后,敌人无论从哪一面察看,反而会认为士兵增加了25名.”随后他画了一张图让大家看(如图)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com