
分析 四边形的两条对角线将四边形分成四个三角形,根据重心的性质可得这四个三角形的重心E,F,G,H连成的四边形是平行四边形,而这个平行四边形又被两条对角线AC和BD分成四块小平行四边形,每块小平行四边形的面积在被AC、BD分得的四个三角形中的比例是一样的,所以只需考查一个小平行四边形与一个三角形面积之比即可.
解答 解:如图: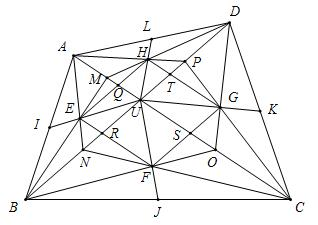
∵E、F分别是△OAB与△OBC的重心,
∴$\frac{BE}{EM}=\frac{BF}{FO}=\frac{2}{1}$,
∴EF∥AC,
同理:FG∥BD,HG∥AC,HE∥BD,
∴ERUQ,RUSF,USGT,THQU,EFGH是平行四边形,
∵$\frac{BE}{BM}=\frac{2}{3}$,∴$\frac{{S}_{△BER}}{{S}_{△BMU}}=\frac{4}{9}$,
同理:$\frac{{S}_{△MEQ}}{{S}_{△BMU}}=\frac{1}{9}$,
∴$\frac{{S}_{ERUQ}}{{S}_{△BMU}}=\frac{4}{9}$,
∴$\frac{{S}_{ERUQ}}{{S}_{△ABU}}=\frac{2}{9}$,
同理:$\frac{{S}_{RUSF}}{{S}_{△BCU}}=\frac{2}{9}$,$\frac{{S}_{USGT}}{{S}_{△CDU}}=\frac{2}{9}$,$\frac{{S}_{THQU}}{{S}_{△ADU}}=\frac{2}{9}$.
∴$\frac{{S}_{EFGH}}{{S}_{ABCD}}=\frac{2}{9}$.
点评 本题考查了重心的性质、平行四边形的判定、相似三角形的判定及性质、面积比例等重要知识点.巧妙利用重心分中线所成比为2:1这一重要性质是关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
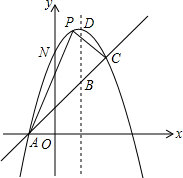 如图,已知抛物线y=-x2+bx+c过(1,4)与(4,-5)两点,且与一直线y=x+1相交于A,C两点,
如图,已知抛物线y=-x2+bx+c过(1,4)与(4,-5)两点,且与一直线y=x+1相交于A,C两点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com