
���� ��1�����ݡ��~״�ı��Ρ��Ķ��弴�������D���꣮
��2������ͼ�Σ������ж���D��������y��ȡֵ��Χ��
��3���������������ۢٵ���P�ڶԽ���AC��ʱ������M����AC�ĶԳƵ�K������KN��AC�ڵ�P����ʱ��PMN���ܳ���С���ڵ���P�ڶԽ���BD��ʱ����PMN���ܳ�����Сֵ�����ڣ�
��� �⣺��1����ͼ1�У�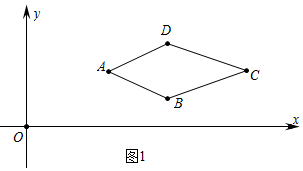
������AC��ֱƽ���߶��߶�BD����֪B��D����ֱ��AC�Գƣ�
��A��3��2����B��5��1����C��8��2����
��D��5��3����
��2����ͼ2�У�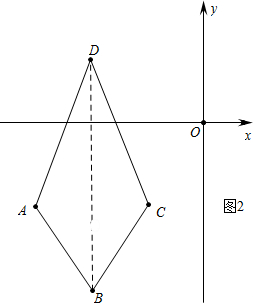
�������֪��BD��ֱƽ���߶�AC��
���ı���ABCD���ı��Σ�A��-6��-3����B��-4��-6����C��-2��-3����
�ඥ��D������y��ȡֵ��Χ��y��-3��
��3����ͼ3�У�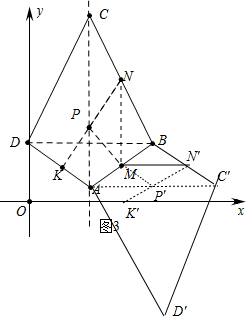
�ٵ���P�ڶԽ���AC��ʱ������M����AC�ĶԳƵ�K������KN��AC�ڵ�P����ʱ��PMN���ܳ���С��
������A��3��1����B��6��3����
�߶Խ���BD=6��
��D��0��3����
��$\frac{1}{2}$��6��AC=30��
��AC=10��
��C��3��11����
��M��4.5��2����N��4.5��7����K��1.5��2��
��MN=5��KN=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$��
��PMN���ܳ�����СֵΪ$\sqrt{34}$+5��
�ڵ�M��N�ֱ���AB��BC����е㣬P��Ϊ�Խ���AC����һ���㣬ͬ�������P��M��N���ܳ�����СֵΪ3+$\sqrt{13}$��
���PMN���ܳ�����Сֵ����$\sqrt{34}$+5��3+$\sqrt{13}$��
���� ���⿼���������ۺ��⡢��Գ�-������⡢���~״�ı��Ρ��Ķ����֪ʶ������Ĺؼ����������⣬ѧ��������Գƽ��������⣬�����п�������Ŀ��


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��105 | B�� | 3��106 | C�� | 30��105 | D�� | 0.3��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
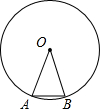 ��ͼ��ABΪ��O���ڽ�������ε�һ�ߣ���֪��OAB=70�㣬�����������ε��ڽǺ�Ϊ1260�㣮
��ͼ��ABΪ��O���ڽ�������ε�һ�ߣ���֪��OAB=70�㣬�����������ε��ڽǺ�Ϊ1260�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{\frac{1}{x}=3}\\{x-y=4}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x+1=3}\\{y+2=-1}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{xy=1}\\{3x-2y=-1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x-3y=3}\\{y=-1}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x+3y=5xy | B�� | a6��a=a5 | C�� | x3•x4=x12 | D�� | ${��\sqrt{3}+2��}^{2}$=7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | $\sqrt{2}$ | D�� | ��$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com