练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
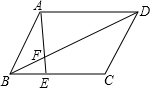
    13．如图，点E是平行四边形ABCD边BC上一点，BE：EC=4：1，AE交BD于F点，BF：FD等于（　　）
    A．4：5B．4：9C．5：9D．4：10

    分析 由平行四边形的性质可证△BEF∽△DAF，再利用相似三角形的性质可求得BE：AD=BF：FD，结合条件可求得答案．

    解答 解：
    ∵四边形ABCD是平行四边形，
    ∴AD∥BC，且AD=BC，
    ∵BE：EC=4：1，
    ∴BE：AD=BE：BC=4：5，
    ∵AD∥BC，
    ∴∠BEF=∠DAF，∠EBF=∠ADF，
    ∴△BEF∽△DAF，
    ∴BF：FD=BE：AD=4：5，
    故选A．

    点评 本题主要考查相似三角形的判定和性质，利用相似三角形的性质把所求问题转化为求BE：AD是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

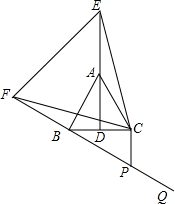    3．如图，在等边△ABC中，已知AD是∠BAC的角平分线，E为AD延长线上一点，以CE为一边且在CE以左作等边△CEF，连接BF．
    （1）求证：AE=BF；
    （2）若BC=8，EC=15，求四边形EFBD的面积．
    （3）在（2）的条件下，延长FB，P为射线FB上一点，CP=5，且∠CPF＜90°，若点Q在射线FB上，且以Q、C、P三点为顶点的三角形是等腰三角形，求CQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图所示，OA⊥OB，OA=45cm，OB=15cm，一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O，机器人立即从B处出发以相同的速度匀速直线前进去拦截小球，在点C处截住了小球，求机器人行走的路程BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列各组中的两个项不属于同类项的是（　　）
    A．3x2y和-2x2yB．a2和32C．-1和$1\frac{1}{4}$D．-xy和2yx

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．在实数-$\frac{22}{7}$、0、-$\sqrt{3}$、506、π、0.0101中，无理数的个数是（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，是学校花圃的一角，有的同学为了省时间图方便，在花圃中踩出了一条“捷径”，“捷径”的数学道理是（　　）
    A．两点确定一条直线B．垂线段最短
    C．两点之间，线段最短D．两点之间，直线最短

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列说法中，正确的是（　　）
    ①射线AB和射线BA是同一条射线；
    ②若AB=BC，则点B为线段AC的中点；
    ③同角的补角相等；
    ④两点之间，线段最短．
    A．①②B．②③C．②④D．③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列说法正确的是（　　）
    A．一组对边平行，另一组对边相等的四边形是平行四边形
    B．对角线互相垂直的四边形四边中点顺次连接成的四边形是矩形
    C．三个角的度数之比为1：$\sqrt{3}$：2的三角形是直角三角形
    D．对角线互相垂直的平行四边形是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．已知函数y=（m-2）x${\;}^{{m}^{2}-2}$+4x+7是二次函数，则m的值为（　　）
    A．-2B．±2C．$\sqrt{3}$D．±$\sqrt{3}$

    查看答案和解析>>

    同步练习册答案