
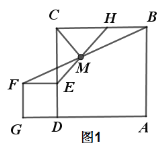
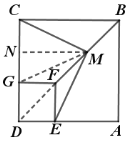
【题目】如图1,点E是正方形ABCD边CD上任意点,以DE为边作正方形DEFG,连接BF.点M是线段BF中点,射线EM与BC交于点H,连接CM.
(1)请直接写出CM和EM的数量关系和位置关系:__________;
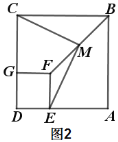
(2)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD上,如图2所示,其他条件不变,(1)中的结论是否成立,请说明理由.
(3)若DG=![]() ,AB=4.
,AB=4.
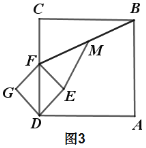
①把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,连接EM,如图3所示,其他条件不变,计算EM的长度;
②若把图1中的正方形DEFG绕点D顺时针旋转一周,请直接写出EM的最大值.
【答案】(1)![]() .(2)成立,具体利用见解析;(3)①
.(2)成立,具体利用见解析;(3)①![]() ;②
;②![]() .
.
【解析】
(1)证明![]() ,得到HM=EM,根据等腰之间三角形的性质即可得到;
,得到HM=EM,根据等腰之间三角形的性质即可得到;
(2)连接DF,MG,作![]() 于N,可证得
于N,可证得![]() ,得到ME=MG,
,得到ME=MG,![]() ,再由M为BF的中点,
,再由M为BF的中点,![]() ,得到GN=NC,进一步可得到,又
,得到GN=NC,进一步可得到,又![]() ,
,![]() ,再由角度的关系可得到
,再由角度的关系可得到![]() ,即可得到结论.
,即可得到结论.
(3)①连接BE,CE,过点E作![]() 于点H,根据正方形的性质可推出
于点H,根据正方形的性质可推出![]() ,
,![]() ,证明
,证明![]() ,进一步可得到△CME是等腰直角三角形,根据之间三角形的性质求解即可.
,进一步可得到△CME是等腰直角三角形,根据之间三角形的性质求解即可.
②由条件可证的△CME为等腰直角三角形,当CE最大时,EM最大,当点E旋转至D点下方时,且C,D,E共线时CE最大,此时CE=![]() ,再根据勾股定理即可求解.
,再根据勾股定理即可求解.
(1)结论:![]() .
.
理由:如图1中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在△FME和△BMH中,
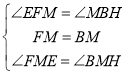 ,
,
∴![]() ,
,
∴HM=EM,EF=BH.
∵CD=BC,
∴CE=CH,
又∵![]() ,HM=EM,
,HM=EM,
∴![]() .
.
(2)![]() .
.
理由:如图,连接DF,MG,作![]() 于N,
于N,
在△EDM和△GDM中,
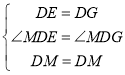 ,
,
∴![]() ,
,
∴ME=MG,![]() ,
,
∵M为BF的中点,![]() ,
,
∴GN=NC,
又![]() ,
,
∴MC=ME,
∴MC=MG,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴(1)中结论成立.
(3)①解:如图,连接BE,CE,过点E作![]() 于点H,
于点H,
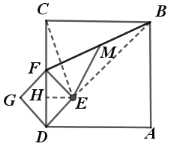
∵四边形ABCD和四边形EDGH是正方形,
∴![]() ,
,![]() ,
,
∴点B、E、D在同一条直线上,
∵![]() ,
,![]() ,M为BF的中点,
,M为BF的中点,
∴![]() ,
,![]() ,
,
∴CM=ME,
又∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△CME是等腰直角三角形,![]() ,
,
在Rt△CME中,![]() ,
,![]() ,
,
∴EH=DH=1,
∴CH=4-1=3,
在Rt△CHE中,![]() ,
,
∴![]() .
.
②由上问可知![]() 一直成立,
一直成立,
∴△CME为等腰直角三角形,
∴当CE最大时,EM最大,
当点E旋转至D点下方时,且C,D,E共线时CE最大,
此时CE=![]() .
.
设CM=EM=x,
则![]() ,
,
解得![]() ,
,
∴EM的最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与x轴负半轴交于点A(-1,0),与y轴正半轴交与点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
的图象与x轴负半轴交于点A(-1,0),与y轴正半轴交与点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
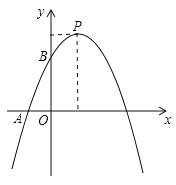
(1) 求一次函数解析式;
(2)求顶点P的坐标;
(3)平移直线AB使其过点P,如果点M在平移后的直线上,且![]() ,求点M坐标;
,求点M坐标;
(4)设抛物线的对称轴交x轴与点E,联结AP交y轴与点D,若点Q、N分别为两线段PE、PD上的动点,联结QD、QN,请直接写出QD+QN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
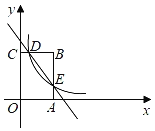
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).反比例函数y=![]() (x>0)的图象经过BC的中点D,与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,与AB交于点E,连接DE.
(1)求k的值;
(2)求直线DE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳卧龙大桥横跨汉江,是我市标志性建筑之一.某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121m,拉索AB与桥面AC的夹角为37°,从点A出发沿AC方向前进23.5m,在D处测得塔冠顶端E的仰角为45°.请你求出塔冠BE的高度(结果精确到0.1m.参考数据sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中数学 来源: 题型:
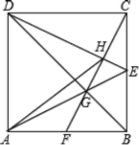
【题目】如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①CF⊥DE;②![]() ;③AD=AH;④GH=
;③AD=AH;④GH=![]() ,其中正确结论的序号是__________.
,其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
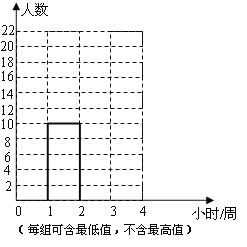
(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据某网站调查,2019年网民最关注的热点话题分别是:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据绘制的统计图如图:
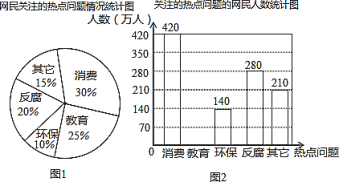
根据以上信息解答下列问题:
(1)请补全条形图,并在图中标明相应数据.
(2)若某市中心城区约有90万人口,请你估计该市中心城区最关注教育问题的人数约有多少万人?
(3)据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年关注该问题网民数的年平均增长率约为多少?(已知2017~2019年每年接受调查的网民人数相同,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com