
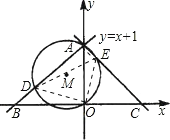
【题目】(12分)如图末-10,在平面直角坐标系中,直线y=x+1与y轴交于点A,与x轴交于点B,点C和点B关于y轴对称.
(1)求△ABC内切圆的半径;
(2)过O、A两点作⊙M,分别交直线AB、AC于点D、E,求证:AD+AE是定值,并求其值.

【答案】(1)![]() -1;(2)
-1;(2)![]()
【解析】试题分析:(1)因为直线y=x+1与y轴交于点A,与x轴交于点B,点C和点B关于y轴对称,所以分别令![]() 即可求出点
即可求出点![]() 的坐标,由此即可求出OA=OB=OC=1,所以可判断
的坐标,由此即可求出OA=OB=OC=1,所以可判断![]() 为Rt△,
为Rt△, ![]() 所以
所以![]() 代入相关数据即可求出内切圆的半径
代入相关数据即可求出内切圆的半径![]() ;
;
(2)连接OD,OE,DE.AE,因为![]() 根据
根据![]() 的圆周角对的弦是直径可得DE为直径,所以
的圆周角对的弦是直径可得DE为直径,所以![]() 又因
又因![]() 利用同角的余角相等可得
利用同角的余角相等可得![]() 因为
因为![]() 且OA=OB.可得△AOE≌△BOD.故AE=BD.所以
且OA=OB.可得△AOE≌△BOD.故AE=BD.所以![]()
试题解析:(1)∵直线AB的解解析式为:y=x+1,
∴A(0,1),B(1,0),
∵点C和点B关于y轴对称,
∴点C(1,0),
∴OA=OB=OC=1,
∵△ABC为Rt△, ![]()
∴![]() ,即内切圆的半径为
,即内切圆的半径为![]()
(2)连接OD,OE,DE.AE,
∵![]()
∴DE为直径.∴![]()
又∵![]()
又∵![]() 且OA=OB.
且OA=OB.
∴△AOE≌△BOD.故AE=BD.
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:

(1)当行使8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
① ________
②____________________________
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题
(1)对角线AC、BD满足条件_____时,四边形EFGH是矩形.
(2)对角线AC、BD满足条件_____时,四边形EFGH是菱形.
(3)对角线AC、BD满足条件_____时,四边形EFGH是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=2,∠A=∠B=30°,点D在线段AB上运动(点D不与A、B重合),连接CD,作∠CDE=30°,DE交BC于点E.
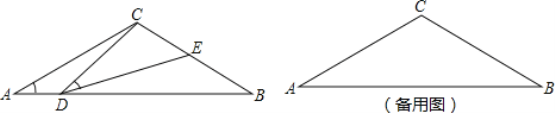
(1)AB=;
(2)当AD等于多少时,△ADC≌△BED,请说明理由;
(3)在点D的运动过程中,△CDE的形状可以是等腰三角形吗?若可以,求出AD的长;若不可以,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当矩形ABCD的长和宽满足什么条件时,四边形MENF是正方形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次排列的3个数:3,9,8,对任相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,![]() ,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,
,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,![]() ,
,![]() ,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?
,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,BF与CE相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)①若四边形EHFG是菱形,则平行四边形ABCD必须满足条件 ;
②若四边形EHFG是矩形,则平行四边形ABCD必须满足条件 .

查看答案和解析>>
科目:初中数学 来源: 题型:
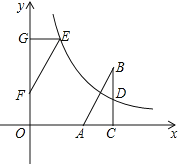
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com