Question

已知一次函数y=kx+b的图象可以看作是由直线y=2x向上平移6个单位长度得到的，且y=kx+b与两坐标轴围成的三角形面积被一正比例函数分成面积的比为1：2的两部分，求这个正比例函数的解析式．

Answer 1

分析：因为y=kx+b的图象是由y=2x向上平移6个单位长度得来的，所以可先求出一次函数的解析式，再由条件与两坐标轴围成的三角形面积被一正比例函数分成面积的比为1：2的两部分可得到S_△AOC不同的值，分别讨论即可．

解答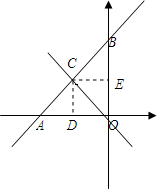：解：y=kx+b的图象是由y=2x向上平移6个单位长度得来的，
∴一次函数的解析式为：y=2x+6，
∴如图，y=2x+6与两坐标轴围成的三角形的面积为
S_△AOB=

1

2

×|-3|×|6|=9，
又∵一正比例函数将它分成面积为1：2的两部分，
∴分成的两三角形面积分别为6，3．
设所求正比例函数与一次函数y=2x+6交于点C，过点C作CD⊥OA于D．
分如下两种情况：
①当S_△AOC=3时，
∵OA=3，∴CD=2，
又∵OB=6，∴CE=2，
∴C（-2，2），
∴这个正比例函数的解析式为y=-x；
②当S_△AOC=6时，
∵OA=3，∴CD=4，
又∵OB=6，∴CE=1．
∴C（-1，4），
∴这个正比例函数的解析式y=-4x．
综上，可知这个正比例函数的解析式为y=-x或y=-4x．

点评：本题考查的是两条直线相交的问题，用函数思想来解决，本题的难点是求出面积，画图是解决的关键．